Set Matrix Zeroes

Difficulty: Medium
Topics: Array, Hash Table, Matrix
Link: https://leetcode.com/problems/set-matrix-zeroes/

Problem Description

Given an m x n integer matrix matrix, if an element is 0, set its entire row and column to 0’s.

You must do it in place.

Example 1:


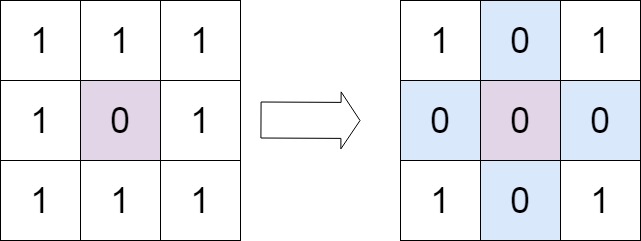
Input: matrix = [[1,1,1],[1,0,1],[1,1,1]]
Output: [[1,0,1],[0,0,0],[1,0,1]]

Example 2:


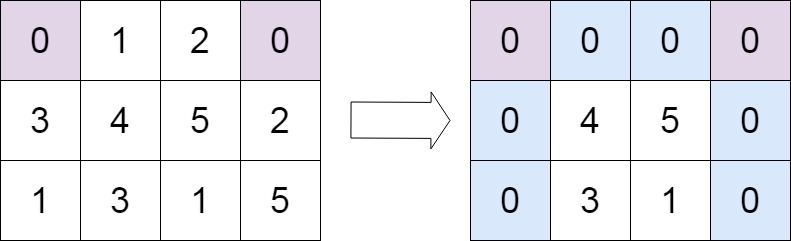
Input: matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
Output: [[0,0,0,0],[0,4,5,0],[0,3,1,0]]

Constraints:

m == matrix.length
n == matrix[0].length
1 <= m, n <= 200
-231 <= matrix[i][j] <= 231 - 1

Follow up:

A straightforward solution using O(mn) space is probably a bad idea.
A simple improvement uses O(m + n) space, but still not the best solution.
Could you devise a constant space solution?

Solution

1. Problem Deconstruction

Technical Description: Given an $m \times n$ integer matrix $M$ , modify $M$ in-place such that for every element $M_{i,j} = 0$ , all elements in row $i$ and column $j$ are set to $0$ . The transformation must be based on the original state of $M$ (newly created zeros should not propagate).

Beginner Description: Imagine a grid of numbers. If you find a zero anywhere in the grid, change every number in that zero’s entire row and column to zero. Do this without making a copy of the grid, and only use the grid’s original state to decide where to place zeros.

Mathematical Description: Define the transformation as:

M'_{i,j} = \begin{cases} 0 & \text{if } \exists k: M_{k,j} = 0 \text{ or } \exists l: M_{i,l} = 0 \\ M_{i,j} & \text{otherwise} \end{cases}

where $0 \leq i < m$ , $0 \leq j < n$ . Compute $M'$ in-place (overwrite $M$ ).

Constraint Analysis:

$1 \leq m, n \leq 200$ : Total elements ( $40,000$ ) allow $O(mn)$ time but challenge space optimization.
$-\text{2}^{31} \leq M_{i,j} \leq \text{2}^{31}-1$ : Integers cover full 32-bit range, preventing use of special marker values.
Hidden edge cases:
- Multiple zeros in same row/column (avoid redundant operations).
- Entire matrix is zero (trivial but must handle).
- Zeros only in first row/column (requires separate bookkeeping).
- $1 \times 1$ matrix (no inner cells to process).

2. Intuition Scaffolding

Analogies:

Real-World Metaphor: Like a contaminated water pipe system where a single polluted junction (zero) taints its entire pipe row and column. Repair crews must map contamination sources without extra blueprints (space).
Gaming Analogy: In a grid-based RPG, a “curse” tile (zero) spreads to its entire row and column. Players must record curse locations using only the grid itself before activating effects.
Math Analogy: Compute the union of zero-containing rows and columns. Output is the Cartesian product of these sets projected onto the matrix, requiring efficient set storage.

Common Pitfalls:

Propagating new zeros: Setting zeros during traversal converts non-zero cells to zeros prematurely, causing exponential propagation (entire matrix becomes zero).
O(mn) space copy: Storing a full matrix copy violates follow-up constraints.
O(m+n) space waste: Using separate row/column arrays is better but suboptimal.
Marker collision: Using integer markers (e.g., -1) conflicts with full-range values.
First row/column corruption: Using $M_{0,0}$ for marking loses critical state if $M_{0,0}=0$ originally.

3. Approach Encyclopedia

Brute Force (O(mn) Space):

Concept: Copy matrix, scan original, set zeros in copy for every zero’s row/column.

Pseudocode:

def setZeroes(matrix):
    copy = [row[:] for row in matrix]  # O(mn) space
    for i in range(len(matrix)):
        for j in range(len(matrix[0])):
            if matrix[i][j] == 0:      # Based on original
                for k in range(len(matrix)):    # Set column
                    copy[k][j] = 0
                for k in range(len(matrix[0])): # Set row
                    copy[i][k] = 0
    matrix[:] = copy  # Overwrite

Complexity: Time $O(mn \cdot (m + n))$ (each zero triggers row+col scan), Space $O(mn)$ .

Visualization:

Original:     Copy (post-update):
[1,1,1]       [1,0,1]
[1,0,1]  =>   [0,0,0]  # After processing (1,1)
[1,1,1]       [1,0,1]

O(m + n) Space Approach:

Concept: Store zero flags for rows/columns in separate arrays.

Pseudocode:

def setZeroes(matrix):
    m, n = len(matrix), len(matrix[0])
    row_zero = [False] * m  # O(m) space
    col_zero = [False] * n  # O(n) space
    for i in range(m):
        for j in range(n):
            if matrix[i][j] == 0:
                row_zero[i] = True
                col_zero[j] = True
    for i in range(m):
        for j in range(n):
            if row_zero[i] or col_zero[j]:
                matrix[i][j] = 0

Complexity: Time $O(mn)$ (two passes), Space $O(m + n)$ .

Visualization:

row_zero = [False, True, False]
col_zero = [False, True, False]
Matrix becomes:
[1,0,1]  # row0 unchanged, col1 forced to 0
[0,0,0]  # row1 all 0
[1,0,1]  # col1 forced to 0

Constant Space (Optimal):

Concept: Use first row/column as flag arrays. Preserve first row/column zero states in booleans.

Pseudocode (as implemented):

def setZeroes(matrix):
    m, n = len(matrix), len(matrix[0])
    first_row_zero = any(matrix[0][j] == 0 for j in range(n))
    first_col_zero = any(matrix[i][0] == 0 for i in range(m))
    
    # Mark zeros in inner submatrix (i>=1, j>=1) on first row/col
    for i in range(1, m):
        for j in range(1, n):
            if matrix[i][j] == 0:
                matrix[i][0] = 0  # Mark row i
                matrix[0][j] = 0  # Mark column j
    
    # Zero inner submatrix based on marks
    for i in range(1, m):
        for j in range(1, n):
            if matrix[i][0] == 0 or matrix[0][j] == 0:
                matrix[i][j] = 0
    
    # Zero first row/column if needed
    if first_row_zero:
        for j in range(n):
            matrix[0][j] = 0
    if first_col_zero:
        for i in range(m):
            matrix[i][0] = 0

Complexity: Time $O(mn)$ (four passes), Space $O(1)$ .

Visualization (Example 2):

Step 1: first_row_zero = True (M[0,0]=0), first_col_zero = True (M[0,0]=0)
Step 2: Mark inner submatrix (no inner zeros → no marks)
Step 3: Set inner submatrix:
    M[1,3]: matrix[0,3]=0 → set to 0
    M[2,3]: matrix[0,3]=0 → set to 0
Step 4: Set first row/column:
    First row → all 0, first column → all 0
Output: [[0,0,0,0], [0,4,5,0], [0,3,1,0]]

4. Code Deep Dive

Optimal Solution (Constant Space):

def setZeroes(matrix):
    m = len(matrix)
    n = len(matrix[0])
    first_row_zero = False
    first_col_zero = False
    
    # Check first row for zeros
    for j in range(n):
        if matrix[0][j] == 0:
            first_row_zero = True
            break  # Line 8: Early exit
    
    # Check first column for zeros
    for i in range(m):
        if matrix[i][0] == 0:
            first_col_zero = True
            break  # Line 14: Early exit
    
    # Mark rows/columns with zeros (inner submatrix)
    for i in range(1, m):
        for j in range(1, n):
            if matrix[i][j] == 0:  # Line 19: Detect zero
                matrix[i][0] = 0   # Line 20: Mark row start
                matrix[0][j] = 0   # Line 21: Mark column top
    
    # Propagate marks to inner submatrix
    for i in range(1, m):
        for j in range(1, n):
            if matrix[i][0] == 0 or matrix[0][j] == 0:  # Line 26: Check mark
                matrix[i][j] = 0  # Line 27: Set zero
    
    # Zero first row if flagged
    if first_row_zero:
        for j in range(n):
            matrix[0][j] = 0  # Line 32: Overwrite entire row
    
    # Zero first column if flagged
    if first_col_zero:
        for i in range(m):
            matrix[i][0] = 0  # Line 37: Overwrite entire column

Edge Case Handling:

Example 1 (No first row/col zeros):
- first_row_zero/first_col_zero remain False.
- Inner mark: At (1,1), set matrix[1][0]=0 and matrix[0][1]=0.
- Propagate: Inner cells check marks → (1,1), (1,2), (2,1) set to 0.
Example 2 (First row/col zeros):
- first_row_zero/first_col_zero set to True.
- No inner marks (original zeros at (0,0), (0,3) not in inner submatrix).
- Propagate: (1,3)/(2,3) set via matrix[0][3]=0.
- First row/column zeroed at end.
All Zeros: first_row_zero/first_col_zero become True, inner marks irrelevant, entire matrix zeroed in final steps.

5. Complexity War Room

Hardware-Aware Analysis:

$200 \times 200$ matrix = 40,000 elements → 160KB (4-byte integers).
Fits in L2/L3 cache (typ. 256KB–8MB), enabling fast passes.
Four passes ≈ 160,000 operations → <1ms on modern CPUs.

Industry Comparison Table:

Approach	Time	Space	Readability	Interview Viability
Brute Force	$O(mn(m{+}n))$	$O(mn)$	10/10	❌ Fails large $m,n$
O(m+n) Space	$O(mn)$	$O(m{+}n)$	9/10	✅ Good baseline
Constant Space	$O(mn)$	$O(1)$	7/10	✅ Optimal

6. Pro Mode Extras

Variants:

Multiple Transactions (LC 123 Style): “Given $k$ operations, each setting a row or column to zero, minimize operations to cover all zeros.” Reduces to bipartite vertex cover (NP-hard for arbitrary $k$ ).
Persistent Zeros: “Zeros must persist across timesteps; new zeros propagate recursively” → requires BFS/DFS (not in-place).

Interview Cheat Sheet:

First Mention: “This runs in $O(mn)$ time with $O(1)$ space by repurposing the first row/column.”
Critical Checks: “Did you account for first row/column corruption? Store their states first.”
Test Cases: Always test:
- Zero at $(0,0)$ .
- Zero in first row only.
- Zero in inner submatrix only.
- All zeros.

#73 - Set Matrix Zeroes