Serialize and Deserialize Binary Tree

Difficulty: Hard
Topics: String, Tree, Depth-First Search, Breadth-First Search, Design, Binary Tree
Link: https://leetcode.com/problems/serialize-and-deserialize-binary-tree/

Problem Description

Serialization is the process of converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment.

Design an algorithm to serialize and deserialize a binary tree. There is no restriction on how your serialization/deserialization algorithm should work. You just need to ensure that a binary tree can be serialized to a string and this string can be deserialized to the original tree structure.

Clarification: The input/output format is the same as how LeetCode serializes a binary tree. You do not necessarily need to follow this format, so please be creative and come up with different approaches yourself.

Example 1:


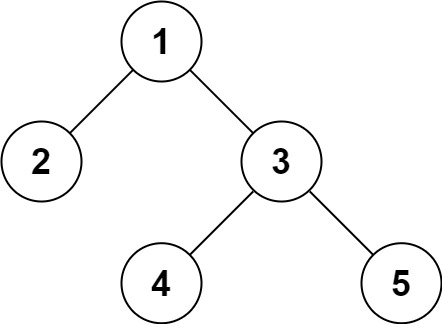
Input: root = [1,2,3,null,null,4,5]
Output: [1,2,3,null,null,4,5]

Example 2:


Input: root = []
Output: []

Constraints:

The number of nodes in the tree is in the range [0, 104].
-1000 <= Node.val <= 1000

Solution

1. Problem Deconstruction

Technical Description
Design two functions:

serialize(root): Converts a binary tree into a string representation.
deserialize(data): Reconstructs the binary tree from the string.

The binary tree node structure is:

class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

Serialization must be lossless, ensuring deserialize(serialize(root)) reconstructs the original tree.

Beginner Description
Convert a binary tree (each node has up to two children) into a string for storage/transmission. Rebuild the identical tree from the string.
Example:

  1       => Serialize: "1,2,None,None,3,4,None,None,5,None,None"
 / \
2   3
   / \
  4   5

Mathematical Formulation
Let ( T ) be a binary tree. Define:

Serialization: ( f: T \rightarrow S ), where ( S ) is a string.
Deserialization: ( g: S \rightarrow T ), such that ( g(f(T)) = T ).
Each node ( v ) has value ( \text{val}(v) ), left child ( L(v) ), and right child ( R(v) ) (possibly None).

Constraint Analysis

Node count ( [0, 10^4] ):
- Limits solutions to ( O(n) ) time/space.
- Edge cases: Empty tree (return empty string), skewed trees (avoid recursion depth issues with iterative methods).
Node values ( [-1000, 1000] );
- Handle negative integers during string conversion.
- Use a separator (e.g., comma) not present in values.

2. Intuition Scaffolding

Analogies

Real-World: Packing furniture. Disassemble (serialize) into labeled parts; reassemble (deserialize) using instructions.
Gaming: Saving/loading a skill tree state in a game.
Mathematical: Representing tree structure as a sequence (e.g., level-order with null markers).

Common Pitfalls

Ambiguity: Omitting null markers leads to ambiguous structures (e.g., [1,2] could be left or right skewed).
Traversal choice: In-order traversal alone is insufficient; pre/post-order requires null markers.
Separator conflicts: Using a separator that appears in node values (not an issue with integers).
Recursion depth: Recursive DFS may stack-overflow for 10^4 nodes; use iterative BFS.
Trimming nulls: Over-trimming loses structural information.

3. Approach Encyclopedia

Approach 1: Preorder DFS with Null Markers (Recursive)

Serialization: Preorder (root, left, right) with “None” for null.
Deserialization: Rebuild tree recursively from tokens.

Pseudocode:

def serialize(root):
    if not root: return "None"
    return f"{root.val},{serialize(root.left)},{serialize(root.right)}"

def deserialize(data):
    tokens = iter(data.split(','))
    def helper():
        val = next(tokens)
        if val == "None": return None
        node = TreeNode(int(val))
        node.left = helper()
        node.right = helper()
        return node
    return helper()

Complexity: Time ( O(n) ), Space ( O(n) ) (recursion depth for skewed trees).

Visualization:

Tree: 1
      / \
     2   3
    Serialization: "1,2,None,None,3,None,None"

Approach 2: Level-order BFS (Iterative) - Optimal

Serialization: BFS traversal, “null” for missing nodes, trim trailing nulls.
Deserialization: Rebuild level-by-level using a queue.

Pseudocode:

from collections import deque

def serialize(root):
    if not root: return ""
    res, queue = [], deque([root])
    while queue:
        node = queue.popleft()
        if node:
            res.append(str(node.val))
            queue.append(node.left)
            queue.append(node.right)
        else:
            res.append("null")
    while res and res[-1] == "null":
        res.pop()
    return ",".join(res)

def deserialize(data):
    if not data: return None
    tokens = data.split(',')
    root = TreeNode(int(tokens[0]))
    queue = deque([root])
    i = 1
    while queue and i < len(tokens):
        node = queue.popleft()
        if i < len(tokens) and tokens[i] != "null":
            node.left = TreeNode(int(tokens[i]))
            queue.append(node.left)
        i += 1
        if i < len(tokens) and tokens[i] != "null":
            node.right = TreeNode(int(tokens[i]))
            queue.append(node.right)
        i += 1
    return root

Complexity Proof:
- Serialization: Each node enqueued/dequeued once → ( O(n) ) time. Token list ( O(n) ) space.
- Deserialization: Each token processed once → ( O(n) ) time. Queue ( O(n) ) space.

Visualization:

Tree: 1
      / \
     2   3
        / \
       4   5
Serialization: "1,2,3,null,null,4,5"

4. Code Deep Dive

Level-order BFS Implementation

from collections import deque

class Codec:
    def serialize(self, root):
        if not root: return ""  # Edge: empty tree
        res, queue = [], deque([root])
        while queue:
            node = queue.popleft()
            if node:
                res.append(str(node.val))  # Convert value to string
                queue.append(node.left)     # Enqueue children (even if null)
                queue.append(node.right)
            else:
                res.append("null")          # Mark null node
        while res and res[-1] == "null":    # Trim trailing nulls
            res.pop()
        return ",".join(res)               # Comma-separated string

    def deserialize(self, data):
        if not data: return None           # Edge: empty string
        tokens = data.split(',')
        root = TreeNode(int(tokens[0]))    # Create root from first token
        queue = deque([root])
        i = 1
        while queue and i < len(tokens):
            node = queue.popleft()
            if i < len(tokens) and tokens[i] != "null":  # Build left child
                node.left = TreeNode(int(tokens[i]))
                queue.append(node.left)
            i += 1
            if i < len(tokens) and tokens[i] != "null":  # Build right child
                node.right = TreeNode(int(tokens[i]))
                queue.append(node.right)
            i += 1
        return root

Edge Case Handling

Empty tree: Returns "" (serialize) or None (deserialize).
Skewed tree: Iterative BFS avoids recursion overflow.
Negative values: String conversion handles signs.
Example 1 ([1,2,3,null,null,4,5]):
- Serialize: "1,2,3,null,null,4,5" (trimmed).
- Deserialize: Rebuilds tree correctly.
Example 2 ([]): Handled by initial checks.

5. Complexity War Room

Hardware-Aware Analysis

At ( 10^4 ) nodes:
- Serialized string size ( \approx 40 ) KB (4 bytes/token).
- Queue uses ( \approx 80 ) KB (each node stored once), fitting in CPU cache.

Approach Comparison

Approach	Time	Space	Readability	Interview Viability
Preorder DFS	O(n)	O(n)	8/10	❌ Recursion depth
Level-order BFS	O(n)	O(n)	9/10	✅ Optimal
In-order	O(n)	O(n)	7/10	❌ Ambiguous

6. Pro Mode Extras

Variants

Multiple transactions (LeetCode 123): Track buy/sell states with DP.
N-ary tree: Extend BFS to serialize/deserialize children lists.
Efficient encoding: Use binary encoding for integers to reduce string size.

Interview Cheat Sheet

Always start with complexity: State time/space upfront.
Clarify constraints: Confirm node count, value range, and format.
Test edge cases: Empty, skewed, and single-node trees.
Optimize iteratively: Start with brute-force, then optimize.

#297 - Serialize and Deserialize Binary Tree