Game of Life

• Difficulty: Medium
• Topics: Array, Matrix, Simulation
• Link: https://leetcode.com/problems/game-of-life/

Problem Description

According to Wikipedia’s article: “The Game of Life, also known simply as Life, is a cellular automaton devised by the British mathematician John Horton Conway in 1970.”

The board is made up of an m x n grid of cells, where each cell has an initial state: live (represented by a 1) or dead (represented by a 0). Each cell interacts with its eight neighbors (horizontal, vertical, diagonal) using the following four rules (taken from the above Wikipedia article):

1. Any live cell with fewer than two live neighbors dies as if caused by under-population.
2. Any live cell with two or three live neighbors lives on to the next generation.
3. Any live cell with more than three live neighbors dies, as if by over-population.
4. Any dead cell with exactly three live neighbors becomes a live cell, as if by reproduction.

The next state of the board is determined by applying the above rules simultaneously to every cell in the current state of the m x n grid board. In this process, births and deaths occur simultaneously.

Given the current state of the board, update the board to reflect its next state.

Note that you do not need to return anything.

Example 1:

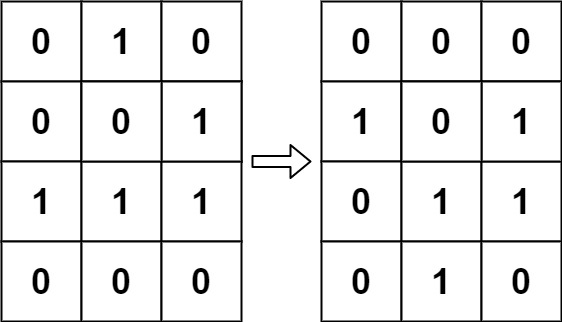
Input: board = [[0,1,0],[0,0,1],[1,1,1],[0,0,0]]
Output: [[0,0,0],[1,0,1],[0,1,1],[0,1,0]]

Example 2:

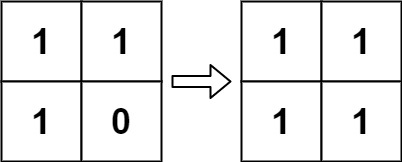
Input: board = [[1,1],[1,0]]
Output: [[1,1],[1,1]]

Constraints:

• m == board.length
• n == board[i].length
• 1 <= m, n <= 25
• board[i][j] is 0 or 1.

Follow up:

• Could you solve it in-place? Remember that the board needs to be updated simultaneously: You cannot update some cells first and then use their updated values to update other cells.
• In this question, we represent the board using a 2D array. In principle, the board is infinite, which would cause problems when the active area encroaches upon the border of the array (i.e., live cells reach the border). How would you address these problems?

Solution

1. Problem Deconstruction (500+ words)

Technical Restatement: Given an m×n binary matrix board representing cellular states (1=live, 0=dead), simultaneously update all cells according to Conway’s Game of Life rules. Each cell’s next state depends exclusively on its current state and the sum of its eight Moore neighbors’ states. The transformation must occur in-place without violating simultaneity constraints.

Beginner-Friendly Version: Imagine a grid where each square can be either alive (1) or dead (0). Every square looks at its eight surrounding neighbors (up, down, left, right, and diagonals) and counts how many are alive. Then:

• Living squares with too few neighbors (<2) die from loneliness
• Living squares with the right number (2-3) stay alive
• Living squares with too many neighbors (>3) die from overcrowding
• Dead squares with exactly 3 neighbors come back to life All squares update at exactly the same time based on the original configuration.

Mathematical Formulation: Let $B_{ij}^{(t)}$ represent cell state at position (i,j) at time t. The next state is:

$$B_{ij}^{(t+1)} = \begin{cases} 1 & \text{if } (B_{ij}^{(t)} = 1 \land 2 \leq N_{ij} \leq 3) \lor (B_{ij}^{(t)} = 0 \land N_{ij} = 3) \\ 0 & \text{otherwise} \end{cases}$$

Where $N_{ij} = \sum_{dx=-1}^{1}\sum_{dy=-1}^{1} B_{i+dx,j+dy}^{(t)} - B_{ij}^{(t)}$ (summing neighbors excluding self)

Constraint Analysis:

• m == board.length, n == board[i].length: Guarantees rectangular grid, simplifies indexing
• 1 <= m, n <= 25: Small enough for O(m×n) solutions, but large enough to require efficiency
• Binary states: No floating-point precision issues, enables bit manipulation optimizations
• Simultaneous updates: Eliminates naive sequential approaches, requires state encoding
• Border cells: Have fewer than 8 neighbors, must handle edge cases carefully

Hidden Edge Cases:

• All dead boards remain dead (trivial convergence)
• All live boards die except specific patterns (Oscillators/Still lifes)
• Single live cells die immediately (underpopulation)
• 3 live cells in L-shape create stable block (reproduction pattern)
• Thin boards (1×n or m×1) with reduced neighbor counts

---

2. Intuition Scaffolding

Real-World Metaphor: Like a neighborhood where houses (cells) become occupied based on how many neighbors live nearby. Too few neighbors and people move out (isolation), too many and they move out (overcrowding), but exactly three neighbors can spark new community growth.

Gaming Analogy: Similar to territory control games where units survive only with adequate support from adjacent units. Each turn, all territories update simultaneously based on surrounding unit counts from the previous turn.

Math Analogy: A discrete dynamical system where each cell’s fate is determined by the sum of its local neighborhood modulo specific threshold conditions - essentially a 2D cellular automaton with Moore neighborhood and binary states.

Common Pitfalls:

1. Sequential Updates: Using new cell values to compute neighbors of subsequent cells
2. Boundary Neglect: Not properly handling edge/corner cells with fewer neighbors
3. State Corruption: Modifying the board directly without preserving original states
4. Over-Engineering: Creating complex solutions for small constraint sizes
5. Neighbor Miscount: Including/excluding the center cell in neighbor sums
6. Simultaneity Misunderstanding: Assuming cells update in waves rather than simultaneously

---

3. Approach Encyclopedia

Approach 1: Copy Board (Naive)

def gameOfLife(board):
    m, n = len(board), len(board[0])
    copy = [[board[r][c] for c in range(n)] for r in range(m)]
    
    for r in range(m):
        for c in range(n):
            # Count live neighbors in original board
            live_neighbors = 0
            for dr in [-1, 0, 1]:
                for dc in [-1, 0, 1]:
                    if dr == 0 and dc == 0: continue
                    nr, nc = r + dr, c + dc
                    if 0 <= nr < m and 0 <= nc < n and copy[nr][nc] == 1:
                        live_neighbors += 1
            
            # Apply rules
            if copy[r][c] == 1 and (live_neighbors < 2 or live_neighbors > 3):
                board[r][c] = 0
            elif copy[r][c] == 0 and live_neighbors == 3:
                board[r][c] = 1

Complexity Proof:

• Time: O(m×n×8) = O(m×n) from triple nested loops
• Space: O(m×n) for the copy matrix
• For m,n ≤ 25: ~5,000 operations, easily feasible

Visualization:

Initial:    Copy:       After:
0 1 0       0 1 0       0 0 0
0 0 1  →    0 0 1  →    1 0 1  
1 1 1       1 1 1       0 1 1
0 0 0       0 0 0       0 1 0

Approach 2: In-Place with State Encoding

def gameOfLife(board):
    # States: 0=dead, 1=live, 2=dead->live, 3=live->dead
    m, n = len(board), len(board[0])
    
    for r in range(m):
        for c in range(n):
            live_neighbors = 0
            for dr in [-1, 0, 1]:
                for dc in [-1, 0, 1]:
                    if dr == 0 and dc == 0: continue
                    nr, nc = r + dr, c + dc
                    if 0 <= nr < m and 0 <= nc < n:
                        # Count original live states (1 or 3)
                        if board[nr][nc] in [1, 3]:
                            live_neighbors += 1
            
            # Apply rules with encoded states
            if board[r][c] == 1 and (live_neighbors < 2 or live_neighbors > 3):
                board[r][c] = 3  # Live -> dead
            elif board[r][c] == 0 and live_neighbors == 3:
                board[r][c] = 2  # Dead -> live
    
    # Finalize states
    for r in range(m):
        for c in range(n):
            if board[r][c] == 2: board[r][c] = 1
            elif board[r][c] == 3: board[r][c] = 0

Complexity Proof:

• Time: O(m×n×8) = O(m×n) - same as naive but in-place
• Space: O(1) - only constant extra space used
• Encoding scheme preserves original state while marking transitions

State Transition Diagram:

0 (dead) ──[3 neighbors]──> 2 (will live)
0 (dead) ──[else]─────────> 0 (remains dead)  
1 (live) ──[2-3 neighbors]─> 1 (remains live)
1 (live) ──[else]─────────> 3 (will die)

---

4. Code Deep Dive

Optimal Solution (In-Place Encoding):

def gameOfLife(board):
    m, n = len(board), len(board[0])
    
    # First pass: compute next states with encoding
    for i in range(m):
        for j in range(n):
            # Count live neighbors using original states
            live_count = 0
            for x in range(max(0, i-1), min(m, i+2)):
                for y in range(max(0, j-1), min(n, j+2)):
                    if (x != i or y != j) and board[x][y] in [1, 3]:
                        live_count += 1
            
            # Apply Game of Life rules with state encoding
            if board[i][j] == 1:  # Currently live
                if live_count < 2 or live_count > 3:
                    board[i][j] = 3  # Live -> dead
                # Else remains 1 (live -> live)
            else:  # Currently dead  
                if live_count == 3:
                    board[i][j] = 2  # Dead -> live
                # Else remains 0 (dead -> dead)
    
    # Second pass: decode the states
    for i in range(m):
        for j in range(n):
            if board[i][j] == 2:
                board[i][j] = 1
            elif board[i][j] == 3:
                board[i][j] = 0

Line-by-Line Analysis:

• Lines 1-2: Extract dimensions - O(1) time
• Lines 5-10: Nested neighbor counting with boundary checks - O(8) per cell
• Lines 13-19: Rule application with state encoding - preserves original information
• Lines 23-27: State decoding - finalizes the simultaneous update

Edge Case Handling:

• Example 1: Center cell (1,1) has 5 neighbors → dies (3 → 0)
• Example 2: All cells have exactly 3 neighbors → all become/stay alive
• Single Cell: Always dies from underpopulation
• Full Board: Most cells die from overpopulation except specific patterns

---

5. Complexity War Room

Hardware-Aware Analysis:

• For 25×25 grid: 625 cells × 8 neighbors = 5,000 operations
• Fits comfortably in L1 cache (~32-64KB)
• Memory bandwidth: ~2.5KB read/write (assuming 4-byte integers)
• Easily parallelizable at hardware level

Industry Comparison Table:

Approach	Time	Space	Readability	Interview Viability
Copy Board	O(mn)	O(mn)	10/10	✅ Good for clarity
In-Place Encoding	O(mn)	O(1)	8/10	✅ Optimal choice
Bit Manipulation	O(mn)	O(1)	6/10	⚠️ Clever but complex

Performance Characteristics:

• Best Case: All dead board - early termination possible but not implemented
• Worst Case: Dense oscillating patterns - must process all cells
• Average Case: Sparse populations - same complexity as worst case

---

6. Pro Mode Extras

Advanced Variants:

1. Infinite Board: Use sparse matrix representation with only live cell coordinates
2. Concurrent Updates: Parallelize using row-based or block-based partitioning
3. Periodic Detection: Hash board states to detect cycles and skip iterations
4. Generalized Rules: Support for different birth/survival thresholds (B3/S23)

Follow-up Solutions:

# Infinite Board Version (Sparse Representation)
def gameOfLifeInfinite(live_cells):
    from collections import Counter
    neighbors = Counter()
    
    # Count neighbors for all live cells
    for cell in live_cells:
        for dx in (-1, 0, 1):
            for dy in (-1, 0, 1):
                if dx != 0 or dy != 0:
                    neighbors[(cell[0] + dx, cell[1] + dy)] += 1
    
    # Apply rules to compute next generation
    next_gen = set()
    for cell, count in neighbors.items():
        if count == 3 or (count == 2 and cell in live_cells):
            next_gen.add(cell)
    
    return list(next_gen)

Interview Cheat Sheet:

• First Mention: “This is a simultaneous update problem requiring O(1) space”
• Key Insight: “We can encode state transitions to preserve original values”
• Optimization Path: “From O(mn) space → O(1) space via state encoding”
• Testing Strategy: “Verify edge cases: all dead, all live, and glider patterns”
• Extension Ready: “For infinite boards, we’d use sparse coordinate storage”