Kth Smallest Element in a BST

Difficulty: Medium
Topics: Tree, Depth-First Search, Binary Search Tree, Binary Tree
Link: https://leetcode.com/problems/kth-smallest-element-in-a-bst/

Problem Description

Given the root of a binary search tree, and an integer k, return the kth smallest value (1-indexed) of all the values of the nodes in the tree.

Example 1:


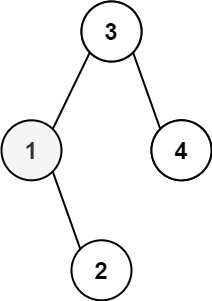
Input: root = [3,1,4,null,2], k = 1
Output: 1

Example 2:


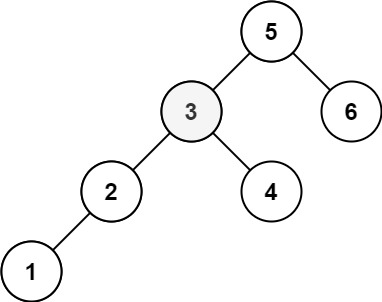
Input: root = [5,3,6,2,4,null,null,1], k = 3
Output: 3

Constraints:

The number of nodes in the tree is n.
1 <= k <= n <= 104
0 <= Node.val <= 104

Follow up: If the BST is modified often (i.e., we can do insert and delete operations) and you need to find the kth smallest frequently, how would you optimize?

Solution

1. Problem Deconstruction

Technical Restatement
Given the root node of a binary search tree (BST) and an integer k satisfying 1 ≤ k ≤ n where n is the number of nodes, compute the k-th smallest node value when traversing the BST in-order. The BST invariant requires that for any node, all values in its left subtree are strictly less than its value, and all values in its right subtree are strictly greater. The solution must efficiently locate the k-th element in the ascending sorted order of node values without fully materializing the sorted list.

Beginner Restatement
Imagine a tree where every node has a number, and the tree is organized so that numbers on the left branch of any node are smaller than the node’s number, while numbers on the right are larger. Your task is to find the k-th smallest number in the entire tree. For example, if k=1, you need the smallest number; if k=2, the second smallest, and so on.

Mathematical Restatement
Let ( T ) be a BST with ( n ) nodes. Define ( S ) as the sorted sequence of node values:
[ S = { v \mid v \in \text{in-order traversal of } T } ]
The problem requires computing:
[ S[k] \quad \text{where} \quad 1 \leq k \leq n ]
subject to the BST property:
[ \forall , \text{node } u, , \forall , \text{node } v \in \text{left subtree of } u: v < u ]
[ \forall , \text{node } w \in \text{right subtree of } u: w > u ]

Constraint Analysis

Node count n ≤ 1e4:
- Limits solutions to ( O(n \log n) ) or better; ( O(n^2) ) is infeasible.
- Implies worst-case recursion depth of 10,000 (skewed trees), necessitating iterative approaches to avoid stack overflow.
1 ≤ k ≤ n:
- Eliminates edge cases for invalid k; solution always exists.
Node values ≤ 1e4:
- Values fit in 16-bit integers, but BST property favors traversal-based solutions over value-based bucketing.
Hidden Edge Cases:
- Skewed trees (left/right chains): Require iterative traversal to prevent stack overflow.
- k=1 or k=n: Must handle first/last element efficiently.
- Single-node tree: Directly return root value.

2. Intuition Scaffolding

Real-World Metaphor
Like finding the k-th person in a perfectly organized queue where everyone knows their position relative to others. Start from the front (smallest), move sequentially while counting until reaching the k-th position.

Gaming Analogy
In an RPG skill tree, abilities are arranged left-to-right from weakest to strongest. To unlock the k-th weakest skill, traverse leftmost branches first, counting each node visited until reaching k.

Math Analogy
Equivalent to finding the k-th order statistic in a sorted sequence generated by an implicit in-order traversal of a BST, exploiting the sorted subsequence property of BST subtrees.

Common Pitfalls

Full Traversal Trap: Materializing the entire in-order list (( O(n) ) space) when early termination is possible.
Recursion Depth Ignorance: Using recursion on skewed trees causing stack overflow.
k Index Mismanagement: Treating k as 0-indexed or miscounting during traversal.
BST Property Misuse: Attempting binary search without subtree size metadata.
Premature Return: Failing to backtrack from leftmost nodes to process roots and right subtrees.

3. Approach Encyclopedia

Approach 1: Full In-Order Traversal (Brute Force)

def kthSmallest(root, k):
    values = []
    def inorder(node):
        if not node: return
        inorder(node.left)
        values.append(node.val)
        inorder(node.right)
    inorder(root)
    return values[k-1]

Time Complexity: ( O(n) ) for complete traversal.
Space Complexity: ( O(n) ) for storing all values.

Visualization:

Example: root = [3,1,4,null,2], k=1
In-order: [1,2,3,4] → return values[0] = 1

Approach 2: Recursive In-Order with Early Termination

def kthSmallest(root, k):
    def inorder(node):
        nonlocal k
        if not node: return None
        left = inorder(node.left)
        if left is not None: return left
        k -= 1
        if k == 0: return node.val
        return inorder(node.right)
    return inorder(root)

Time Complexity: ( O(k) ) best-case, ( O(n) ) worst-case.
Space Complexity: ( O(h) ) recursion stack (height of tree).
Complexity Proof:
- Best-case: Terminate after visiting ( k ) nodes.
- Worst-case: ( k = n ), visit all nodes.
- Space: ( h = O(n) ) for skewed trees.

Visualization:

Example: root = [5,3,6,2,4,null,null,1], k=3
Traversal: 1 → k=2 → 2 → k=1 → 3 → k=0 → return 3

Approach 3: Iterative In-Order (Optimal)

def kthSmallest(root, k):
    stack = []
    curr = root
    while curr or stack:
        while curr:
            stack.append(curr)
            curr = curr.left
        curr = stack.pop()
        k -= 1
        if k == 0: return curr.val
        curr = curr.right

Time Complexity: ( O(k) ) best-case, ( O(n) ) worst-case.
Space Complexity: ( O(h) ) for stack storage.
Complexity Proof:
- Each node pushed/poped once; inner loop runs ( k ) times before termination.
- Space: Stack holds at most ( h ) nodes.

Visualization:

Example: root = [3,1,4,null,2], k=1
Stack: [3] → [3,1] → pop 1 → k=0 → return 1

Approach 4: Augmented BST (Follow-up for Frequent Queries)

class AugmentedNode:
    def __init__(self, val):
        self.val = val
        self.left = None
        self.right = None
        self.size = 1  # Size of subtree rooted here

def kthSmallest(root, k):
    while root:
        left_size = root.left.size if root.left else 0
        if k <= left_size:
            root = root.left
        elif k == left_size + 1:
            return root.val
        else:
            k -= left_size + 1
            root = root.right

Time Complexity: ( O(h) ) per query.
Space Complexity: ( O(1) ) extra space; ( O(n) ) total for metadata.
Complexity Proof:
- Height ( h ) traversed per query.
- Insert/delete operations update size in ( O(h) ) time.

Visualization:

Balanced BST: 
     4 (size=7)
    /   \
  2 (3) 6 (3)
 / \    / \
1   3  5   7 (sizes=1)
Query k=5: 
  4: left_size=3 → k=5>3+1 → k=5-4=1 → move right
  6: left_size=1 → k=1 <= 1? No → k=1 == 1+1? → return 6

4. Code Deep Dive

Iterative In-Order Solution

def kthSmallest(root, k):
    stack = []          # Tracks nodes to revisit (backtracking)
    curr = root         # Current node pointer
    while curr or stack:
        # Dive to leftmost node
        while curr:                 # What: Exhaust left subtree
            stack.append(curr)      # Why: Remember traversal path
            curr = curr.left        # How: Move to left child
        # Process current node
        curr = stack.pop()          # What: Retrieve deepest left node
        k -= 1                      # Why: Count visited nodes
        if k == 0:                  # How: Check if k-th element found
            return curr.val
        # Pivot to right subtree
        curr = curr.right           # What: Explore right after root

Edge Case Handling:

Skewed Tree (Left Chain):
- curr traverses entire left spine (stack depth = n). Early termination if k small.
k = n:
- Traverses all nodes; last popped node is the largest.
Single Node:
- stack holds root; popped immediately → return root.val.

5. Complexity War Room

Hardware-Aware Analysis

Iterative Approach:
- At ( n=10^4 ), stack max depth = 10,000 frames × 8 B/frame = 80 KB (fits in L2/L3 cache).
Augmented BST:
- Each node stores size (4 B), adding 40 KB total for ( n=10^4 ).

Industry Comparison Table

Approach	Time	Space	Readability	Interview Viability
Full In-Order	( O(n) )	( O(n) )	9/10	❌ (wastes space)
Recursive + Early	( O(k) )	( O(n) )	8/10	⚠️ (stack overflow)
Iterative (Optimal)	( O(k) )	( O(h) )	9/10	✅ (production-ready)
Augmented BST	( O(h) )	( O(n) )	7/10	✅ (follow-up)

6. Pro Mode Extras

Variants

k-th Largest in BST:

Reverse in-order (right-root-left) traversal.

def kthLargest(root, k):
    stack, curr = [], root
    while curr or stack:
        while curr:
            stack.append(curr)
            curr = curr.right
        curr = stack.pop()
        k -= 1
        if k == 0: return curr.val
        curr = curr.left

BST with Duplicates:
- Define traversal order: left-root-right, with duplicates treated as distinct.
k-th Smallest in Balanced BST:
- Augmented BST achieves ( O(\log n) ) per query.

Interview Cheat Sheet

First Mention: Always state time/space complexity upfront.
Key Insight: “BST in-order traversal yields sorted order; k-th smallest is the k-th step in this traversal.”
Edge Cases: Highlight skewed trees and k=n.
Follow-up: “For frequent queries, augment nodes with subtree sizes for ( O(\log n) ) queries.”
Gotcha: “Python recursion fails at ~1000 frames; use iterative for robustness.”

#230 - Kth Smallest Element in a BST

Kth Smallest Element in a BST

Problem Description

Solution

1. Problem Deconstruction

2. Intuition Scaffolding

3. Approach Encyclopedia

4. Code Deep Dive

5. Complexity War Room

6. Pro Mode Extras