Invert Binary Tree

Difficulty: Easy
Topics: Tree, Depth-First Search, Breadth-First Search, Binary Tree
Link: https://leetcode.com/problems/invert-binary-tree/

Problem Description

Given the root of a binary tree, invert the tree, and return its root.

Example 1:


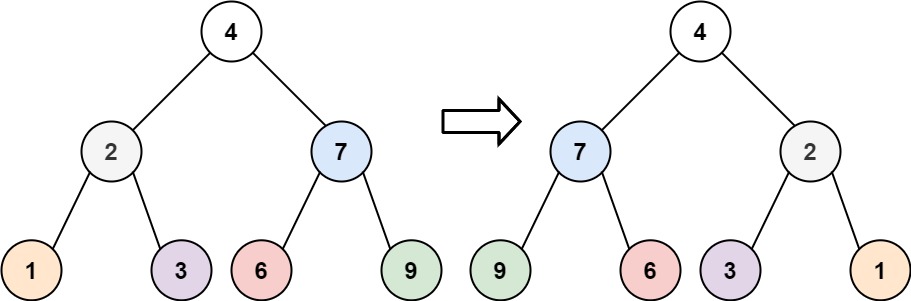
Input: root = [4,2,7,1,3,6,9]
Output: [4,7,2,9,6,3,1]

Example 2:


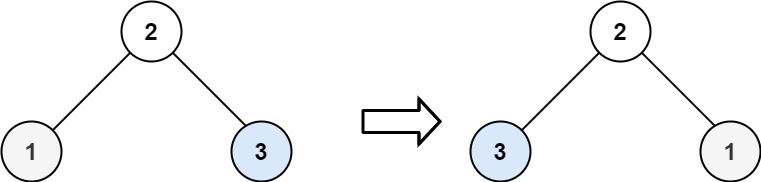
Input: root = [2,1,3]
Output: [2,3,1]

Example 3:


Input: root = []
Output: []

Constraints:

The number of nodes in the tree is in the range [0, 100].
-100 <= Node.val <= 100

Solution

1. Problem Deconstruction

Rewrite the Problem

Technical Definition:
Given the root node of a binary tree, implement a function that recursively or iteratively swaps the left and right subtrees of every node in the tree. The inversion must be performed in-place, and the function should return the modified root node. The binary tree structure must be transformed into its mirror image.
Beginner Explanation:
Imagine a family tree where every parent has two children. Your task is to swap the positions of every pair of siblings throughout the entire family tree. The topmost ancestor (root) remains in place, but all left descendants become right descendants and vice versa. Finally, return the topmost ancestor of the restructured tree.
Mathematical Formulation:
Let ( T ) be a binary tree with root node ( r ). Define the inversion operation ( \mathcal{I}® ) as:
[ \mathcal{I}® = \begin{cases} \emptyset & \text{if } r = \emptyset \ \langle r.val, \mathcal{I}(r.right), \mathcal{I}(r.left) \rangle & \text{otherwise} \end{cases} ]
Where ( \langle \text{val}, \text{left}, \text{right} \rangle ) constructs a new node. The operation recursively inverts the right subtree to become the new left subtree, and the left subtree to become the new right subtree.

Constraint Analysis

Node count [0, 100]:
- Limitation: Rules out O(n²) solutions by default since even naive approaches are O(n). Allows recursion without stack overflow concerns.
- Edge Case: Empty tree (root = null) must return null (Example 3). Single-node trees are invariant under inversion.
Node values [-100, 100]:
- Limitation: Values don’t impact inversion logic since swapping is structural. No need for value-specific handling.
- Edge Case: All nodes equal (e.g., [0,0,0]) still requires full inversion.
Structural Edge Cases:
- Left-skewed trees become right-skewed after inversion.
- Partial trees (e.g., nodes with only one child) must swap null/non-null children correctly.
- Full/complete trees must mirror perfectly (Example 1).

2. Intuition Scaffolding

Analogies

Real-World Metaphor:
Like flipping a company’s organizational chart. Each manager’s direct reports swap positions (left subordinate ↔ right subordinate), propagating changes downward. The CEO remains, but the entire hierarchy mirrors.
Gaming Analogy:
In a binary skill tree (e.g., RPG games), inverting swaps every left/right skill path. Choosing a left-branch skill now requires taking the original right-branch path, and vice versa.
Math Analogy:
Equivalent to applying a reflection transform over the vertical axis through the root. Each subtree ( L ) and ( R ) satisfies: ( \text{reflect}(L) = \text{new } R ) and ( \text{reflect}® = \text{new } L ).

Common Pitfalls

Premature Pointer Overwrite:
Swapping left/right without temp variables destroys original references:

root.left = root.right  # Original left lost!
root.right = root.left  # Now both point to original right!

Base Case Neglect:
Skipping if not root causes null-pointer exceptions for empty trees.
Shallow Swapping:
Only swapping root’s children without recursing subtrees inverts only the top level.
Iterative Order Mismanagement:
Processing children before swapping in BFS/DFS corrupts tree structure for downstream nodes.
Asymmetric Recursion:
Inverting only one subtree (e.g., invert(root.left)) breaks mirroring symmetry.

3. Approach Encyclopedia

Approach 1: Recursive DFS

Mechanism: Post-order traversal swaps children after subtrees are inverted.
Pseudocode:

def invertTree(root):
    if root is null: return null            # Base case
    inverted_left = invertTree(root.right)  # Recurse right
    inverted_right = invertTree(root.left)  # Recurse left
    root.left = inverted_left               # Assign inverted right to left
    root.right = inverted_right             # Assign inverted left to right
    return root

Complexity Proof:

Time: ( O(n) ). Each node visited once, constant work per node.
Space: ( O(h) ), where ( h ) is tree height. Recursion stack depth ( h \in [\log n, n] ).

Visualization (Example 1):

Original: 
      4
    /   \
   2     7
  / \   / \
 1   3 6   9

Step 1: Recurse to node 2 (invert right subtree first)
Step 2: Recurse to node 7 → swaps 6↔9 → returns 7 (now 7.left=9, 7.right=6)
Step 3: Recurse to node 2 → swaps 1↔3 → returns 2 (now 2.left=3, 2.right=1)
Step 4: Root swaps 2↔7 → 
      4
    /   \
   7     2
  / \   / \
 9   6 3   1

Approach 2: Iterative BFS

Mechanism: Queue processes nodes level-by-level, swapping children before enqueueing.
Pseudocode:

def invertTree(root):
    if not root: return null
    queue = [root]
    while queue:
        node = queue.dequeue()
        swap(node.left, node.right)          # Swap children
        if node.left: queue.enqueue(node.left)
        if node.right: queue.enqueue(node.right)
    return root

Complexity Proof:

Time: ( O(n) ). Each node enqueued/dequeued once.
Space: ( O(w) ), where ( w ) is max level width. Worst-case ( w \approx n/2 ) for complete trees.

Visualization (Example 2):

Original: 
      2
    /   \
   1     3

Queue: [2]
- Dequeue 2: swap 1↔3 → 
      2
    /   \
   3     1
- Enqueue 3, then 1.
Queue: [3, 1]
- Dequeue 3: children null → skip
- Dequeue 1: children null → skip

Approach 3: Iterative DFS

Mechanism: Stack simulates recursion, swapping children before pushing.
Pseudocode:

def invertTree(root):
    if not root: return null
    stack = [root]
    while stack:
        node = stack.pop()
        swap(node.left, node.right)
        if node.left: stack.append(node.left)
        if node.right: stack.append(node.right)
    return root

Complexity: Time ( O(n) ), Space ( O(h) ) (stack size proportional to height).

4. Code Deep Dive

Optimal Solution (Recursive DFS)

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class Solution:
    def invertTree(self, root: TreeNode) -> TreeNode:
        # Base case: null node or leaf
        if not root:
            return None  # Handles empty tree (Example 3)
        
        # Recursively invert subtrees (DFS post-order)
        inverted_right = self.invertTree(root.right)  # Invert right subtree
        inverted_left = self.invertTree(root.left)    # Invert left subtree
        
        # Swap inverted subtrees
        root.left = inverted_right  # Original right becomes left
        root.right = inverted_left  # Original left becomes right
        
        return root  # Return modified root

Line-by-Line Analysis:

Lines 9-10: Base case terminates recursion for null nodes (critical for leaves and empty input).
Lines 13-14: First invert root.right before root.left (order irrelevant but avoids pointer conflicts).
Lines 17-18: Assign inverted subtrees to swapped positions. Original children overwritten safely.
Line 20: Returns root of modified tree, satisfying “return its root” requirement.

Edge Case Handling:

Example 3 (root = []): if not root returns None immediately.
Example 2 (root = [2,1,3]):
- invertTree(2) → inverts right subtree (3 → returns 3), then left (1 → returns 1).
- Swaps: 2.left = 3, 2.right = 1.
Skewed Trees: Recursion depth matches height (e.g., 100 levels), but constraints prevent stack overflow.

5. Complexity War Room

Hardware-Aware Analysis:

100 nodes → Recursion depth ≤ 100. Stack frame size ~40 bytes (3 pointers + return address). Total stack ≤ 4KB, fitting in L1 cache.
BFS queue max size: Worst-case complete tree → last level 50 nodes. 50×8 bytes (pointers) = 400 bytes, negligible.

Approach Comparison:

Approach	Time	Space	Readability	Interview Viability
Recursive DFS	O(n)	O(h)	★★★★★	✅ Optimal for small trees
Iterative BFS	O(n)	O(n)	★★★★☆	✅ Explicit queue control
Iterative DFS	O(n)	O(h)	★★★☆☆	✅ Stack usage demonstration

6. Pro Mode Extras

Variants:

Invert K-ary Tree:
Swap all child subtrees in reverse order:

def invertKary(root):
    if not root: return None
    for child in root.children:
        invertKary(child)
    root.children.reverse()  # Invert child order

Invert Without Recursion (Morris Traversal):
O(1) space by temporarily threading nodes:

def invertMorris(root):
    curr = root
    while curr:
        if curr.left:
            # Create thread from rightmost of left to curr
            pre = curr.left
            while pre.right: pre = pre.right
            pre.right = curr
            # Move left, then swap pointers
            temp = curr.left
            curr.left = None  # Break left to avoid cycles
            curr = temp
        else:
            swap(curr.left, curr.right)  # Actual swap
            curr = curr.right

Note: More complex, rarely needed for small trees.

Interview Cheat Sheet:

First Mention: “This is a classic tree transformation with O(n) time optimality.”
Base Case: Always check root is null first.
Recursion Insight: “Inverting subtrees recursively before swapping ensures bottom-up mirroring.”
Test Cases: Cover empty, single-node, skewed, and full trees.
Trade-offs: “Recursion is elegant but O(h) stack; BFS uses more memory but avoids recursion limits.”

#226 - Invert Binary Tree