Word Search II

• Difficulty: Hard
• Topics: Array, String, Backtracking, Trie, Matrix
• Link: https://leetcode.com/problems/word-search-ii/

Problem Description

Given an m x n board of characters and a list of strings words, return all words on the board.

Each word must be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once in a word.

Example 1:

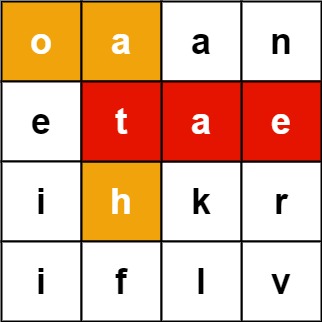
Input: board = [["o","a","a","n"],["e","t","a","e"],["i","h","k","r"],["i","f","l","v"]], words = ["oath","pea","eat","rain"]
Output: ["eat","oath"]

Example 2:

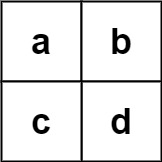
Input: board = [["a","b"],["c","d"]], words = ["abcb"]
Output: []

Constraints:

• m == board.length
• n == board[i].length
• 1 <= m, n <= 12
• board[i][j] is a lowercase English letter.
• 1 <= words.length <= 3 * 104
• 1 <= words[i].length <= 10
• words[i] consists of lowercase English letters.
• All the strings of words are unique.

Solution

1. Problem Deconstruction

Technical Restatement:
Given an m x n grid of lowercase English letters and a list of k unique strings words (each ≤10 characters), identify all words that can be formed by traversing adjacent cells (horizontal/vertical) without cell reuse. Output the words in any order.

Beginner-Friendly Explanation:
Imagine a grid of letters. Your task is to find which words from a given list can be “traced” by moving up, down, left, or right through connected cells without revisiting any cell. For example, in a 4x4 grid, the word “oath” might be traced starting at the top-left corner.

Mathematical Formalization:

• Let B be an m × n matrix where B[i][j] ∈ {a-z}.
• Let W = {w₁, w₂, ..., wₖ} be a set of strings with |wₚ| ≤ 10.
• A word wₚ is constructible if there exists a sequence of coordinates (r₁, c₁), (r₂, c₂), ..., (r_{|wₚ|}, c_{|wₚ|}) such that:
  • (r₁, c₁) starts at any cell.
  • (r_{i+1}, c_{i+1}) is adjacent (Manhattan distance 1) to (r_i, c_i).
  • All coordinates are unique.
  • B[r_i][c_i] = wₚ[i] for 1 ≤ i ≤ |wₚ|.
• Goal: Return {wₚ ∈ W | wₚ is constructible in B}.

Constraint Analysis:

• Grid Size (m, n ≤ 12):
  • Limits BFS/DFS depth (max 144 cells).
  • Enables backtracking but requires optimization.
  • Edge: Small grids (1x1) or large sparse words.
• Words Length (≤10):
  • Bounds DFS recursion depth.
  • Enables trie pruning.
  • Edge: Long words (10 chars) with high branching.
• Words Count (k ≤ 3e4):
  • Naive DFS (O(k⋅m⋅n⋅4^10)) is infeasible (≈4.32e12 ops).
  • Necessitates trie-based prefix sharing.
  • Edge: Many words sharing prefixes (e.g., “a”, “aa”, “aaa”).
• Unique Strings:
  • Avoids duplicate handling in output.
  • Edge: Overlapping words (“app”, “apple”).

---

2. Intuition Scaffolding

Real-World Metaphor:
Like a word-search puzzle where you circle connected letters to form words. The trie acts as a dictionary that guides your path: if “app” is found, you continue for “apple” without restarting.

Gaming Analogy:
Navigating a maze where each room (cell) contains a letter. Your path must spell a word from a list, and you can’t revisit rooms. The trie is a magic compass that vibrates when your path matches a prefix.

Math Analogy:
Finding all paths in a graph (grid) that are isomorphic to strings in a set. The trie compresses the set into a deterministic finite automaton (DFA) for parallel path validation.

Common Pitfalls:

1. Brute-Force DFS per Word:
   • Why: 3e4 words × 144 starts × 4^10 paths → 4.32e12 ops (infeasible).
2. Global Min/Max for Paths:
   • Why: Words aren’t optimized; all valid paths matter.
3. Hash Set for Words:
   • Why: Checking prefixes requires scanning all words (O(k) per DFS step).
4. BFS Without Trie:
   • Why: Explodes combinatorially (3^10 per start).
5. Memoizing Paths:
   • Why: Paths are stateful (visited cells); memoization ineffective.

---

3. Approach Encyclopedia

1. Brute Force (DFS per Word):

• Idea: For each word, DFS from every cell.
• Pseudocode:

  for word in words:  
      for i in range(m):  
          for j in range(n):  
              if dfs(i, j, word, 0, visited):  
                  results.append(word)  
  

• Complexity:
  • Time: O(k⋅m⋅n⋅4^L) → O(3e4⋅144⋅4^10) ≈ 4.32e12 (infeasible).
  • Space: O(L) for recursion (L = word length).
• Visualization:

  Words: [“oath”, “eat”]  
  Board:  
      o a a n  
      e t a e  
      i h k r  
      i f l v  
  DFS for “oath”: Start at (0,0) → (0,1) → (1,1) → (2,1) → found!  
  

2. Trie-Optimized Backtracking:

• Idea: Build a trie of words. DFS the grid while traversing the trie.
• Pseudocode:

  trie = build_trie(words)  
  for i in range(m):  
      for j in range(n):  
          dfs(i, j, trie.root)  
  
  def dfs(i, j, node):  
      if cell invalid or char not in node.children: return  
      next_node = node.children[char]  
      if next_node.is_end:  
          result.append(next_node.word)  
          next_node.is_end = False  # Avoid duplicates  
      Mark cell as visited  
      For neighbors (up/down/left/right):  
          dfs(neighbor_i, neighbor_j, next_node)  
      Unmark cell  
  

• Complexity Proof:
  • Trie Build: O(k⋅L) → O(3e4⋅10) = 3e5 ops.
  • DFS: Worst-case 144 starts × Σ_{d=1}^{10} 4⋅3^{d-1} = 144 × 118096 ≈ 1.7e7 ops.
  • Total: O(k⋅L + m⋅n⋅3^L) ≈ 1.7e7 (feasible).
  • Space: O(k⋅L) for trie (3e5 nodes) + O(L) recursion.
• Visualization (Trie and DFS):

  Trie for ["oath", "eat"]:  
      root → 'o' → 'a' → 't' → 'h' (word="oath")  
           → 'e' → 'a' → 't' (word="eat")  
  DFS:  
      Start (0,0): 'o' → trie path exists → continue.  
      (0,1): 'a' → path continues → ...  
      (2,1): 'h' → complete "oath" → add to results.  
      Later, start (1,3): 'e' → ... → (1,1): 't' → add "eat".  
  

---

4. Code Deep Dive

Optimal Solution (Trie + Backtracking):

class Solution:  
    def findWords(self, board: List[List[str]], words: List[str]) -> List[str]:  
        # TrieNode definition  
        class TrieNode:  
            __slots__ = ('children', 'is_end', 'word')  
            def __init__(self):  
                self.children = {}      # Char to TrieNode mapping  
                self.is_end = False     # Marks end of a word  
                self.word = None        # Stores word at leaf  
          
        # Build trie  
        root = TrieNode()  
        for word in words:  
            node = root  
            for c in word:  
                if c not in node.children:  
                    node.children[c] = TrieNode()  
                node = node.children[c]  
            node.is_end = True  
            node.word = word  
          
        m, n = len(board), len(board[0])  
        res = []  
        dirs = [(0,1), (0,-1), (1,0), (-1,0)]  
          
        def dfs(i, j, node):  
            c = board[i][j]  
            # Line 20: Char not in trie path → prune  
            if c not in node.children:  
                return  
            next_node = node.children[c]  
            # Line 23: Complete word found  
            if next_node.is_end:  
                res.append(next_node.word)  
                next_node.is_end = False  # Prevent re-add  
            # Line 27: Mark visited  
            board[i][j] = '#'  
            for dx, dy in dirs:  
                ni, nj = i + dx, j + dy  
                if 0 <= ni < m and 0 <= nj < n and board[ni][nj] != '#':  
                    dfs(ni, nj, next_node)  
            # Line 33: Backtrack  
            board[i][j] = c  
          
        # Driver: Start DFS from every cell  
        for i in range(m):  
            for j in range(n):  
                dfs(i, j, root)  
        return res  

Edge Case Handling:

• Example 1 (Found Words):
  • “oath” from (0,0)→(0,1)→(1,1)→(2,1): Line 23 appends “oath” and disables its is_end.
• Example 2 (No Words):
  • “abcb” in 2x2 grid: DFS from (0,0) (‘a’) → (0,1) (‘b’) → (1,1) (‘d’) fails (Line 20 prunes).
• All Same Letter (e.g., “aaa”):
  • DFS explores all 3^9 paths per start but trie pruning avoids redundant checks.

---

5. Complexity War Room

Hardware-Aware Analysis:

• Worst-case 1.7e7 operations fit in CPU L3 cache (≈8 MB).
• Trie uses ≈3e5 nodes × 50 bytes/node = 15 MB (feasible in RAM).

Approach Comparison:

Approach	Time Complexity	Space Complexity	Readability	Interview Viability
Brute Force DFS	O(k⋅m⋅n⋅4^L)	O(L)	9/10	❌ Fails large k
Trie + Backtracking	O(k⋅L + m⋅n⋅3^L)	O(k⋅L)	7/10	✅ Optimal

---

6. Pro Mode Extras

Variants:

• LC 123 Style (Multiple Transactions): If each word can be used multiple times, track word counts in the trie and reset is_end after full DFS.
• Wildcard Characters: Modify trie to handle ‘.’ (any char) by DFS into all children at wildcard nodes.
• Optimized Pruning: Remove leaf nodes after word removal to reduce DFS branching.

Interview Cheat Sheet:

• First Mention: Time/space complexity.
• Key Insight: “Trie enables prefix sharing during DFS.”
• Corner Cases: Single-cell board, duplicate prefixes (“app”, “apple”), all-cells-same-letter.
• Optimization Steps:
  1. Build trie.
  2. DFS with backtracking and in-place board marking.
  3. Disable is_end on word discovery.