Merge Two Sorted Lists

• Difficulty: Easy
• Topics: Linked List, Recursion
• Link: https://leetcode.com/problems/merge-two-sorted-lists/

Problem Description

You are given the heads of two sorted linked lists list1 and list2.

Merge the two lists into one sorted list. The list should be made by splicing together the nodes of the first two lists.

Return the head of the merged linked list.

Example 1:

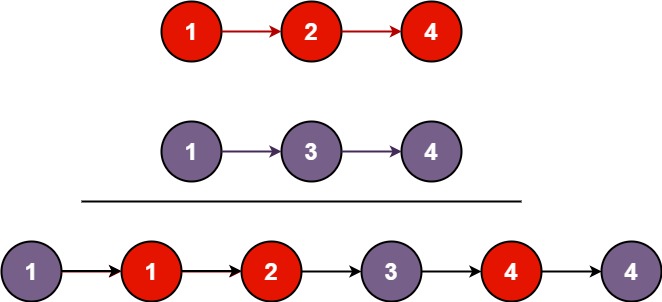
Input: list1 = [1,2,4], list2 = [1,3,4]
Output: [1,1,2,3,4,4]

Example 2:

Input: list1 = [], list2 = []
Output: []

Example 3:

Input: list1 = [], list2 = [0]
Output: [0]

Constraints:

• The number of nodes in both lists is in the range [0, 50].
• -100 <= Node.val <= 100
• Both list1 and list2 are sorted in non-decreasing order.

Solution

1. Problem Deconstruction

Technical Definition:
Given two singly linked lists list1 and list2, each sorted in non-decreasing order, merge them into a single sorted linked list by splicing their nodes (without creating new nodes). Return the head of the merged list.

Beginner Explanation:
You have two lines of sorted numbers (like sorted train cars). Combine them into one sorted line by connecting the cars in order. Always pick the smallest available car from either line to attach next.

Mathematical Formulation:

• Let $L_1 = (a_1, a_2, \dots, a_m)$ and $L_2 = (b_1, b_2, \dots, b_n)$ be sorted sequences ($a_i \leq a_{i+1}$, $b_j \leq b_{j+1}$).
• The merged list $M$ must satisfy $M_k \leq M_{k+1}$ for all $k$, constructed as:
  • $M_1 = \min(L_1[0], L_2[0])$
  • $M_{k} = \begin{cases} \min(L_1[i], L_2[j]) & \text{if } i < m \text{ and } j < n \\ L_1[i] & \text{if } j = n \\ L_2[j] & \text{if } i = m \end{cases}$
    where $i$ and $j$ are pointers advancing when their value is chosen.

Constraint Analysis:

1. Node count $[0, 50]$:
   • Limits algorithmic choices: $O(n^2)$ is acceptable but $O(n)$ is optimal.
   • Edge: Empty lists → return None.
2. Values $[-100, 100]$:
   • Comparisons are safe; negatives and duplicates are handled.
   • Edge: Duplicates (e.g., $1 \leq 1$) must preserve order.
3. Non-decreasing order:
   • Enables $O(n)$ merge via pointer traversal.
   • Edge: Single-node lists merge trivially.

---

2. Intuition Scaffolding

Real-World Analogy (File Sorting):
Two alphabetized stacks of files. Repeatedly pick the topmost file from the stack starting with the earlier letter, forming a new sorted stack.

Gaming Analogy (Unit Deployment):
Two queues of game units sorted by strength. Deploy the weakest available unit from either queue at each step.

Math Analogy (Merge in Merge Sort):
The fundamental merge step in divide-and-conquer sorting, combining two sorted subarrays into one.

Common Pitfalls:

1. Ignoring empty lists: Returns None incorrectly if one list is empty.
2. Creating new nodes: Violates splicing requirement by allocating memory.
3. Pointer advancement failure: Forgetting to move pointers after attaching a node.
4. Incomplete attachment: Not linking the remainder of the non-empty list.
5. Recursive stack overflow: Using recursion for large lists (irrelevant here per constraints).

---

3. Approach Encyclopedia

Approach 1: Iterative with Dummy Node (Optimal)

Pseudocode:

def mergeTwoLists(list1, list2):  
    dummy = ListNode(-1)       # Placeholder node  
    current = dummy            # Pointer for merged list  
    while list1 and list2:      # Both lists have nodes  
        if list1.val <= list2.val:  
            current.next = list1   # Attach list1 node  
            list1 = list1.next     # Move list1 pointer  
        else:  
            current.next = list2   # Attach list2 node  
            list2 = list2.next     # Move list2 pointer  
        current = current.next     # Move merged list pointer  
    current.next = list1 or list2  # Attach remaining nodes  
    return dummy.next              # Return head of merged list  

Complexity Proof:

• Time: $O(n + m)$. Each node is visited exactly once.
• Space: $O(1)$. Only dummy node and pointers used.

Visualization:

Step 0:  
  list1: 1 → 2 → 4  
  list2: 1 → 3 → 4  
  dummy → Ø, current = dummy  

Step 1 (list1.val(1) ≤ list2.val(1)):  
  current.next → list1(1)  
  list1 → 2 → 4, current → 1  

Step 2 (list1.val(2) > list2.val(1)):  
  current.next → list2(1)  
  list2 → 3 → 4, current → 1  

Step 3 (list1.val(2) ≤ list2.val(3)):  
  current.next → list1(2)  
  list1 → 4, current → 2  

Step 4 (list1.val(4) > list2.val(3)):  
  current.next → list2(3)  
  list2 → 4, current → 3  

Step 5:  
  Attach remaining: current.next → list1(4)  
  Final: 1 → 1 → 2 → 3 → 4 → 4  

Approach 2: Recursive

Pseudocode:

def mergeTwoLists(list1, list2):  
    if not list1: return list2     # Base: list1 exhausted  
    if not list2: return list1     # Base: list2 exhausted  
    if list1.val <= list2.val:  
        list1.next = mergeTwoLists(list1.next, list2)  # Recurse  
        return list1  
    else:  
        list2.next = mergeTwoLists(list1, list2.next)  # Recurse  
        return list2  

Complexity Proof:

• Time: $O(n + m)$. Each recursive call processes one node.
• Space: $O(n + m)$. Recursion stack depth.

Approach 3: In-place Iterative (No Dummy)

Pseudocode:

def mergeTwoLists(list1, list2):  
    if not list1: return list2  
    if not list2: return list1  
    head = None  
    # Pick head from list1/list2 (smaller val)  
    if list1.val <= list2.val:  
        head = list1  
        list1 = list1.next  
    else:  
        head = list2  
        list2 = list2.next  
    current = head  
    # Merge remaining nodes iteratively  
    while list1 and list2:  
        if list1.val <= list2.val:  
            current.next = list1  
            list1 = list1.next  
        else:  
            current.next = list2  
            list2 = list2.next  
        current = current.next  
    current.next = list1 or list2  
    return head  

Complexity: Same as Approach 1 but more edge cases.

---

4. Code Deep Dive

Optimal Solution (Iterative with Dummy):

class ListNode:  
    def __init__(self, val=0, next=None):  
        self.val = val  
        self.next = next  

def mergeTwoLists(list1: ListNode, list2: ListNode) -> ListNode:  
    dummy = ListNode(-1)  # Dummy node for edge-free start  
    current = dummy       # Pointer to build merged list  
    while list1 and list2:  
        if list1.val <= list2.val:  # Choose smaller node  
            current.next = list1    # Attach list1 node  
            list1 = list1.next      # Advance list1 pointer  
        else:  
            current.next = list2    # Attach list2 node  
            list2 = list2.next      # Advance list2 pointer  
        current = current.next      # Move current pointer  
    current.next = list1 if list1 else list2  # Attach leftovers  
    return dummy.next  # Skip dummy, return actual head  

Edge Case Handling:

• Example 2 ([] + [] → []):
  • list1/list2 are None → loop skipped → current.next = None → return dummy.next = None.
• Example 3 ([] + [0] → [0]):
  • Loop skipped → current.next = list2 → returns 0 node.
• Partial exhaustion:
  • Loop exits when one list ends → current.next attaches the other list.

---

5. Complexity War Room

Hardware-Aware Analysis:

• At max 50 nodes:
  • Memory: $50 \times (4\text{-byte val} + 8\text{-byte pointer}) \approx 600$ bytes → fits in L1 cache.
  • Time: $50 + 50 = 100$ operations → negligible.

Industry Comparison:

Approach	Time	Space	Readability	Interview Viability
Dummy Iterative	$O(n+m)$	$O(1)$	10/10	✅ Ideal
Recursive	$O(n+m)$	$O(n+m)$	8/10	✅ (small $n$)
In-place (no dummy)	$O(n+m)$	$O(1)$	6/10	⚠️ (edge cases)

---

6. Pro Mode Extras

Variants:

1. Merge $k$ Sorted Lists (Leetcode 23):
   • Use a min-heap to track heads of all lists → pop smallest → push next.
   • Time: $O(N \log k)$, $N$ = total nodes, $k$ = number of lists.
2. Merge with $O(1)$ Space (In-place):
   • Modify pointers without dummy node (as in Approach 3).
3. Merge in Reverse Order:
   • Merge normally → reverse result ($O(n)$ time) or recursively attach larger nodes.

Interview Cheat Sheet:

• First Steps:
  1. Confirm edge cases (empty lists).
  2. Propose dummy node for cleaner code.
• Key Insight: Splicing nodes $\equiv$ pointer manipulation.
• Always Mention: Time ($O(n+m)$)/space ($O(1)$) upfront.
• Avoid: New node creation; recursion for large inputs.