Remove Nth Node From End of List

• Difficulty: Medium
• Topics: Linked List, Two Pointers
• Link: https://leetcode.com/problems/remove-nth-node-from-end-of-list/

Problem Description

Given the head of a linked list, remove the nth node from the end of the list and return its head.

Example 1:

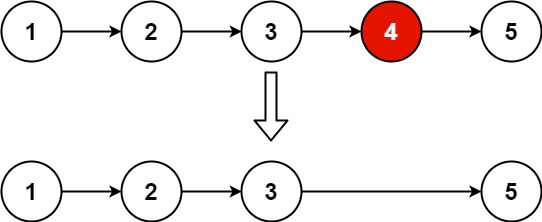
Input: head = [1,2,3,4,5], n = 2
Output: [1,2,3,5]

Example 2:

Input: head = [1], n = 1
Output: []

Example 3:

Input: head = [1,2], n = 1
Output: [1]

Constraints:

• The number of nodes in the list is sz.
• 1 <= sz <= 30
• 0 <= Node.val <= 100
• 1 <= n <= sz

Follow up: Could you do this in one pass?

Solution

1. Problem Deconstruction

Technical Restatement

Given the head node of a singly linked list and an integer n, remove the node positioned n places from the end of the list. Return the modified list’s head. Constraints:

• List size sz satisfies 1 ≤ sz ≤ 30.
• Node values: 0 ≤ val ≤ 100.
• n satisfies 1 ≤ n ≤ sz.
  The core challenge is achieving this with a single traversal (follow-up).

Beginner Explanation

Imagine a conga line of people holding shoulders. You know the first person (head). Your task: remove the person who is n positions from the end. After removal, reconnect the line. For example:

• Line: Alice → Bob → Charlie → Dave → Eve (n=2). Remove Dave (2nd from end). New line: Alice → Bob → Charlie → Eve.
• If the line has 1 person (n=1), return an empty line.

Mathematical Formulation

Let the list be a sequence of nodes: $L = [v_1, v_2, \dots, v_k]$ where $k = \text{sz}$. Remove node at position $p = k - n + 1$ (1-indexed). The new list is:
$L_{\text{new}} = [v_1, \dots, v_{p-1}, v_{p+1}, \dots, v_k]$
Return $v_1$ (or None if $k=1$ and $n=1$).

Constraint Analysis

• 1 ≤ sz ≤ 30:
  • Limits solution space; even $O(\text{sz}^2)$ is acceptable.
  • Edge: Single-node list removal → return None.
• 0 ≤ Node.val ≤ 100:
  • Values are non-negative and bounded; no impact on algorithm design.
• 1 ≤ n ≤ sz:
  • Guarantees n is valid. Critical edge: n = sz (remove head) or n = 1 (remove tail).

---

2. Intuition Scaffolding

Analogies

1. Real-World (Queue Management):
   A store queue (30 people max). Manager wants to remove the n-th person from the end. Use two assistants:
   • Assistant A starts at the front, walks n+1 positions ahead.
   • Assistant B starts at the front. Both walk at same speed. When A reaches the end, B is behind the target. Remove B’s next person.
2. Gaming (Snake Segment Removal):
   In a snake game, remove the n-th segment from the tail. Place two markers:
   • Marker 1: n+1 segments ahead of Marker 2.
   • Move both toward the tail. When Marker 1 hits the tail, Marker 2 is before the target.
3. Mathematical (Fixed Offset):
   Let $d$ = distance between two pointers. Set $d = n + 1$. When the leading pointer traverses $k$ nodes (reaching None), the trailing pointer is at position $k - d = k - (n + 1)$. The target is at $k - n + 1$ (1-indexed).

Common Pitfalls

1. Head Removal Edge Case:
   If n = sz, the head must be removed. Solution: Use a dummy head to unify logic.
2. Off-by-One in Pointer Gap:
   Setting gap to n (not n+1) lands the trailing pointer on the target, making removal impossible.
3. Single-Node List:
   Forgetting to return None after removal.
4. Null Pointer in Traversal:
   Accessing next of None when n is larger than list size (handled by constraints).
5. Two-Pass Inefficiency:
   Counting nodes first (pass 1) then removing (pass 2) fails the one-pass follow-up.

---

3. Approach Encyclopedia

Approach 1: Two-Pass (Brute Force)

Pseudocode:

def removeNthFromEnd(head, n):  
    sz = 0  
    curr = head  
    while curr:           # Pass 1: Count nodes  
        sz += 1  
        curr = curr.next  
    target_idx = sz - n   # 0-indexed position to remove  
    if target_idx == 0:   # Remove head  
        return head.next  
    curr = head  
    for _ in range(target_idx - 1):  # Traverse to node before target  
        curr = curr.next  
    curr.next = curr.next.next       # Remove target  
    return head  

Complexity Proof:

• Time: $O(2k) = O(k)$. Pass 1: $k$ nodes. Pass 2: Up to $k - n$ nodes.
• Space: $O(1)$.
  Visualization:

Example: [1,2,3,4,5], n=2  
Pass 1: Count = 5 → target_idx = 3 (0-indexed value=4).  
Pass 2: Traverse to index 2 (node 3):  
  1 → 2 → 3 → 4 → 5  
          |        |  
          +--------+   → 1 → 2 → 3 → 5  

Approach 2: One-Pass (Two Pointers)

Pseudocode:

def removeNthFromEnd(head, n):  
    dummy = ListNode(0, head)  # Dummy head  
    first = second = dummy  
    for _ in range(n + 1):     # Create n+1 gap  
        first = first.next  
    while first:                # Traverse until first is None  
        first = first.next  
        second = second.next  
    second.next = second.next.next  # Remove target  
    return dummy.next  

Complexity Proof:

• Time: $O(k)$. first traverses $(n+1) + (k - n) = k + 1$ nodes.
• Space: $O(1)$.
  Visualization:

Example: [1,2,3,4,5], n=2, k=5  
Step 1: Dummy(0) → 1 → 2 → 3 → 4 → 5  
        second   first (after n+1=3 steps: first at 3)  
Step 2: Move both until first=None:  
        0 → 1 → 2 → 3 → 4 → 5 → None  
                    second   first  
Step 3: Remove second.next (4):  
        0 → 1 → 2 → 3 → 5  

---

4. Code Deep Dive

Optimal Solution (One-Pass)

class Solution:  
    def removeNthFromEnd(self, head: Optional[ListNode], n: int) -> Optional[ListNode]:  
        dummy = ListNode(0, head)  # Dummy node to simplify head removal  
        first = second = dummy      # Initialize pointers  
        for _ in range(n + 1):      # Create gap of n+1 nodes  
            first = first.next  
        while first:                # Traverse until first hits end  
            first = first.next  
            second = second.next  
        second.next = second.next.next  # Remove target node  
        return dummy.next  # Return new head (skips dummy)  

Line-by-Line Annotations

1. dummy = ListNode(0, head):
   • What: Sentinel node pointing to head.
   • Why: Unifies head removal (when n = sz) with other cases.
2. first = second = dummy:
   • What: Initialize pointers at dummy.
   • Why: Synchronized start for gap creation.
3. for _ in range(n + 1):
   • What: Advance first by n+1 nodes.
   • Why: Creates fixed gap of n+1 so second lands before the target.
4. while first:
   • What: Move both pointers until first is None.
   • Why: When first reaches end, second is before the target.
5. second.next = second.next.next:
   • What: Skip the target node.
   • Why: Removes the node at position k - n + 1.
6. return dummy.next:
   • What: Return head of modified list.
   • Why: dummy.next points to new head (handles removal of original head).

Edge Case Handling

• Example 2 (Single Node):
  head = [1], n=1.
  • dummy(0) → 1 → None.
  • first moves 2 steps: to 1 then None.
  • while first skipped → second at dummy.
  • dummy.next = None → return None.
• Head Removal (n = sz):
  head = [1,2,3,4,5], n=5.
  • After gap creation, first at None.
  • second at dummy → remove dummy.next (original head).
  • New head: dummy.next.next = 2.

---

5. Complexity War Room

Hardware-Aware Analysis

• At sz=30, memory:
  • Nodes: 30 × (4B val + 8B pointer) = 360B.
  • Pointers: 3 × 8B = 24B.
    Total: < 400B → Fits in L1 CPU cache.

Approach Comparison

Approach	Time	Space	Readability	Interview Viability
Two-Pass	O(k)	O(1)	★★★★★★★★☆☆ (8/10)	✅ (but not one-pass)
One-Pass	O(k)	O(1)	★★★★★★★☆☆☆ (7/10)	✅ (optimal)

---

6. Pro Mode Extras

Variants

1. Remove from Beginning:
   Traverse to (n-1)-th node and remove next.
2. Two Transactions (LC 123):
   Extension: Track max profit with two buys/sells. Requires DP with states.
3. Circular List:
   Use fast-slow pointers to detect cycle, then adjust removal logic.

Interview Cheat Sheet

• Key Insight: Two pointers with fixed gap handle “n-th from end”.
• Must-Mention: Dummy node for edge cases, one-pass efficiency.
• Time/Space: Always state first.
• Verify: Test n=1, n=sz, and single-node cases.