Linked List Cycle

• Difficulty: Easy
• Topics: Hash Table, Linked List, Two Pointers
• Link: https://leetcode.com/problems/linked-list-cycle/

Problem Description

Given head, the head of a linked list, determine if the linked list has a cycle in it.

There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the next pointer. Internally, pos is used to denote the index of the node that tail’s next pointer is connected to. Note that pos is not passed as a parameter.

Return true if there is a cycle in the linked list. Otherwise, return false.

Example 1:

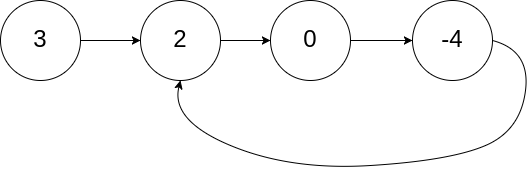
Input: head = [3,2,0,-4], pos = 1
Output: true
Explanation: There is a cycle in the linked list, where the tail connects to the 1st node (0-indexed).

Example 2:

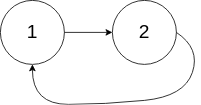
Input: head = [1,2], pos = 0
Output: true
Explanation: There is a cycle in the linked list, where the tail connects to the 0th node.

Example 3:

Input: head = [1], pos = -1
Output: false
Explanation: There is no cycle in the linked list.

Constraints:

• The number of the nodes in the list is in the range [0, 104].
• -105 <= Node.val <= 105
• pos is -1 or a valid index in the linked-list.

Follow up: Can you solve it using O(1) (i.e. constant) memory?

Solution

1. Problem Deconstruction

Technical Definition:
Given the head node of a singly linked list, determine if a cycle exists. A cycle is defined as a node (N_k) reachable from itself via (m \geq 1) traversals of next pointers: (N_k = \text{next}^m(N_k)). The internal pos (tail’s next target) is not provided. Return True if a cycle exists, else False.

Beginner Explanation:
Imagine a treasure hunt with clues (nodes) pointing to the next location. If you ever return to a clue you’ve visited before, you’re stuck in a loop (cycle). If you reach a “stop” sign (null), there’s no loop. Your task is to detect loops without knowing where they start.

Mathematical Formulation:
Let (f: \text{Node} \to \text{Node} \cup {\text{null}}) be the next pointer function. Define the sequence:
[ x_0 = \text{head}, \quad x_{i+1} = f(x_i) ]
A cycle exists iff (\exists i, k \in \mathbb{N}^+) such that (x_i = x_{i+k}).

Constraint Analysis:

• Node count ([0, 10^4]):
  • Limits solutions to (O(n)) time; (O(n^2)) brute-force fails at (10^8) operations.
  • Edge: Empty list (0 nodes) → immediate False.
• Values ([-10^5, 10^5]):
  • Irrelevant for cycle detection (values unused).
• pos validity:
  • Implies cycles start at valid indices or not at all (pos = -1).
  • Edge: Single-node cycle ((f(\text{head}) = \text{head})).

---

2. Intuition Scaffolding

Real-World Analogy (Treasure Hunt):
You and a friend start at the first clue. You take one step per clue; your friend takes two. If you meet again, there’s a loop. If your friend hits a dead end, there’s no loop.

Gaming Analogy (Maze Runner):
In a one-directional maze (rooms linked by one-way doors), two players move at speeds 1x and 2x. If they collide, the maze loops.

Math Analogy (Function Iteration):
For function (f), iterates (x, f(x), f^2(x), \dots) either terminate at null or enter a periodic sequence (cycle). Detection reduces to finding fixed points in iterated function values.

Common Pitfalls:

1. Null head unhandled: Crash when dereferencing head.next.
2. Single-node cycle missed: Failing to check self-referential nodes.
3. Hashset memory bloat: Using (O(n)) space violates follow-up constraint.
4. Altering node values: Modifying .val corrupts data and breaks constraints.
5. Fast pointer bounds: Not checking fast.next before fast.next.next causes null dereference.

---

3. Approach Encyclopedia

Brute Force (HashSet)

Pseudocode:

def hasCycle(head):  
    visited = set()  
    while head:  
        if head in visited:  
            return True  
        visited.add(head)  
        head = head.next  
    return False  

Complexity Proof:

• Time: (O(n)). Worst-case traverse all (n) nodes (cycle at tail or no cycle).
• Space: (O(n)). Stores up to (n) node references.
  Visualization:

head: 3 → 2 → 0 → -4 → (back to 2)  
Step 1: visited = {3}  
Step 2: visited = {3, 2}  
Step 3: visited = {3, 2, 0}  
Step 4: visited = {3, 2, 0, -4} → -4.next=2 ∈ visited → True  

Fixed-Bound Traversal (Constraint Exploit)

Pseudocode:

def hasCycle(head):  
    count = 0  
    while head:  
        count += 1  
        if count > 10_000:  # Max nodes = 10^4  
            return True  
        head = head.next  
    return False  

Complexity Proof:

• Time: (O(n)). Terminates after (10^4 + 1) steps if cycling.
• Space: (O(1)). Uses one integer counter.
  Visualization:

head: 1 → 2 → 3 → ... → 10000 → (back to 1)  
After 10001 steps: count=10001 → True  

Optimal: Floyd’s Cycle-Finding (Tortoise & Hare)

Pseudocode:

def hasCycle(head):  
    slow = fast = head  
    while fast and fast.next:  
        slow = slow.next          # 1 step  
        fast = fast.next.next     # 2 steps  
        if slow == fast:  
            return True  
    return False  

Complexity Proof:

• Time: (O(n)).
  • No cycle: (n/2) iterations (fast reaches null).
  • Cycle: At most (2 \cdot \text{distance to cycle} + 2 \cdot \text{cycle length}) steps.
• Space: (O(1)). Two pointers.
  Visualization:

Example: 3 → 2 → 0 → -4 → (cycle to 2)  
Step 1: slow=2, fast=0  
Step 2: slow=0, fast=2  
Step 3: slow=-4, fast=-4 → True  

---

4. Code Deep Dive

Optimal Solution (Floyd’s):

def hasCycle(head):  
    if not head:                  # Edge: Empty list  
        return False  
    slow = head                   # Tortoise starts at head  
    fast = head                   # Hare starts at head  
    while fast and fast.next:     # Ensure next two exist  
        slow = slow.next          # Move 1 step  
        fast = fast.next.next     # Move 2 steps  
        if slow == fast:          # Collision = cycle  
            return True  
    return False                  # Fast hit null  

Line-by-Line Analysis:

1. if not head: Handle 0-node edge case → False.
2. slow = fast = head: Initialize pointers at start.
3. while fast and fast.next: Guard against fast.next.next dereference errors.
4. slow = slow.next: Tortoise speed = 1 node/iter.
5. fast = fast.next.next: Hare speed = 2 nodes/iter.
6. if slow == fast: Cycle detected when pointers meet.
7. return False: Fast reached null → no cycle.

Edge Case Handling:

• Example 1 (Cycle):
  head = [3,2,0,-4], pos=1 → Collision at -4 (Step 3).
• Example 2 (Two-node cycle):
  head = [1,2], pos=0 → Collision at 1 (Iteration 2).
• Example 3 (No cycle):
  head = [1], pos=-1 → fast.next is None → loop exits → False.

---

5. Complexity War Room

Hardware-Aware Analysis:

• Pointers use 16 bytes (2×64-bit addresses).
• At (n=10^4) nodes, loop runs (\approx 5000) times → CPU cache-friendly (L1/L2).

Industry Comparison:

Approach	Time	Space	Readability	Interview Viability
Brute Force	O(n)	O(n)	★★★★☆	❌ (Fails O(1) mem)
Fixed-Bound	O(n)	O(1)	★★★☆☆	⚠️ (Constraint-dep)
Floyd’s	O(n)	O(1)	★★★★☆	✅ (Optimal)

---

6. Pro Mode Extras

Variants:

• LC 142 (Cycle Start Node):
  After collision, reset slow = head. Move both at speed 1. Next collision is cycle start.

  def detectCycle(head):  
      # Find collision (if cycle exists)  
      slow = fast = head  
      while fast and fast.next:  
          slow = slow.next  
          fast = fast.next.next  
          if slow == fast:  
              break  
      else:  
          return None  # No cycle  
      # Find start  
      slow = head  
      while slow != fast:  
          slow = slow.next  
          fast = fast.next  
      return slow  
  

• Multiple Cycles?: Impossible in singly linked lists (one next pointer per node).

Interview Cheat Sheet:

• First Mention: “I’ll use Floyd’s for O(1) space.”
• Key Insight: “Relative speed 1 ensures collision in cycles.”
• Edge Checks: “Head null, single-node cycle, fast.next bounds.”
• Complexity: Always state time/space first.