Binary Tree Maximum Path Sum

Difficulty: Hard
Topics: Dynamic Programming, Tree, Depth-First Search, Binary Tree
Link: https://leetcode.com/problems/binary-tree-maximum-path-sum/

Problem Description

A path in a binary tree is a sequence of nodes where each pair of adjacent nodes in the sequence has an edge connecting them. A node can only appear in the sequence at most once. Note that the path does not need to pass through the root.

The path sum of a path is the sum of the node’s values in the path.

Given the root of a binary tree, return the maximum path sum of any non-empty path.

Example 1:


Input: root = [1,2,3]
Output: 6
Explanation: The optimal path is 2 -> 1 -> 3 with a path sum of 2 + 1 + 3 = 6.

Example 2:


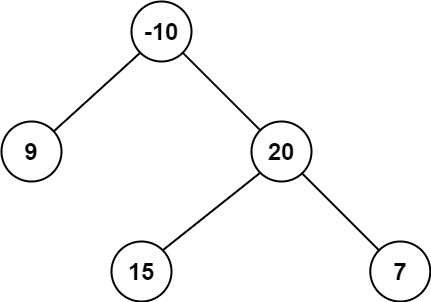
Input: root = [-10,9,20,null,null,15,7]
Output: 42
Explanation: The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.

Constraints:

The number of nodes in the tree is in the range [1, 3 * 104].
-1000 <= Node.val <= 1000

Solution

1. Problem Deconstruction

Technical Definition:
Given a binary tree where each node has an integer value (positive or negative), compute the maximum possible sum of any non-empty path. A path is defined as a sequence of distinct nodes connected by edges where adjacent nodes share a parent-child relationship. The path need not include the root and can start/end at any node. The solution must efficiently handle large trees (up to 30,000 nodes) and negative values.

Beginner Explanation:
Imagine a family tree where each person has a value (like money they contribute). Your task is to find the most valuable connected group of people. The group must form an unbroken chain (parent-child-grandchild, etc.), but you can start and end anywhere. The challenge is to compute the highest possible sum of values in such a chain.

Mathematical Formulation:
Let ( T ) be a binary tree with nodes ( v_1, v_2, \ldots, v_n ), each with value ( \text{val}(v_i) ). A path ( P = (v_{k_1}, v_{k_2}, \ldots, v_{k_m}) ) satisfies:

Adjacency: ( (v_{k_j}, v_{k_{j+1}}) ) share an edge ( \forall j ).
Uniqueness: ( v_{k_j} ) appears at most once.
The path sum is ( \sum_{j=1}^{m} \text{val}(v_{k_j}) ).
Objective:
[ \max_{\text{non-empty } P} \left( \sum_{v \in P} \text{val}(v) \right) ]

Constraint Analysis:

Node count ( \in [1, 3 \times 10^4] ):
- Limits solutions to ( O(n) ) or ( O(n \log n) ). ( O(n^2) ) is infeasible (90M operations worst-case).
- Implies skewed trees → recursion depth up to 30k (risky in Python). Requires iterative DFS or tail recursion optimization.
Node values ( \in [-1000, 1000] ):
- Negative values force handling of “lossy” segments. Single-node paths may dominate if all values are negative.
- Edge case: Entirely negative trees → solution is (\max(\text{node values})).
- Paths may bridge positive subtrees via negative nodes if net gain is positive.

2. Intuition Scaffolding

Real-World Metaphor:
A toll road network where cities (nodes) have tolls (values). Find the most profitable contiguous drive (path) without revisiting cities. Negative tolls force detour decisions.

Gaming Analogy:
In an RPG skill tree, each node grants a bonus/penalty. Activate a connected path for cumulative effects. Maximize bonus while navigating penalties.

Math Analogy:
Tree-adapted Kadane’s algorithm. At each node, compute max “straight” path (linear chain) and “bent” path (forking through the node). Global max aggregates local decisions.

Common Pitfalls:

Root Fixation: Assuming the path must include the root (counter: Example 2).
Negative Mishandling: Clamping gains to 0 prematurely (may discard single negative nodes).
Suboptimal Branching: Taking both children naively breaks path contiguity for ancestors.
Initialization Errors: Setting global max to 0 (fails for all-negative trees).
Overlooked Forked Paths: Missing paths spanning left and right subtrees (e.g., 15→20→7 in Example 2).

3. Approach Encyclopedia

Brute Force (Theoretical):

Idea: For each node, compute all downward paths. For ( v_i ), traverse subtree to find max path through ( v_i ).

Pseudocode:

def brute_force(root):
    def dfs(node, current_sum):
        nonlocal global_max
        if not node: 
            return
        current_sum += node.val
        global_max = max(global_max, current_sum)
        dfs(node.left, current_sum)
        dfs(node.right, current_sum)
        current_sum -= node.val  # Backtrack

    global_max = -inf
    for each node in tree:  # O(n) nodes
        dfs(node, 0)        # O(n) per node → O(n²)
    return global_max

Complexity: Time ( O(n^2) ), Space ( O(h) ).
Derivation: ( n ) nodes, each triggering a DFS of ( O(\text{subtree size}) ). Worst-case subtree size ( O(n) ) → ( \sum_{i=1}^{n} O(n) = O(n^2) ).

Visualization (Skewed Tree):

Root: 1
 │
 └─2
    │
    └─3
       │
       └─... → 30k nodes
Path calculations per node: 30k, 29.9k, ... → ~450M ops (infeasible).

Optimal Approach (Recursive DFS):

Idea: Postorder traversal. At each node:
1. Compute max straight path gains from left/right children (negative → 0).
2. Update global max with path through node + both children.
3. Return max straight path (node + max child gain) for parent reuse.

Pseudocode:

def maxPathSum(root):
    global_max = -inf
    def max_gain(node):
        nonlocal global_max
        if not node: 
            return 0
        left_gain = max(0, max_gain(node.left))    # Skip if negative
        right_gain = max(0, max_gain(node.right))
        # Update global max for paths using node as root
        global_max = max(global_max, node.val + left_gain + right_gain)
        # Return max straight path for parent
        return node.val + max(left_gain, right_gain)
    max_gain(root)
    return global_max

Complexity: Time ( O(n) ), Space ( O(h) ).
Derivation: Each node visited once. Recursion depth = tree height ( h ). Worst-case ( h = n ) (skewed tree).

Visualization (Example 2):

Steps:
  Node 9:  gain=9 → global_max=9
  Node 15: gain=15 → global_max=15
  Node 7:  gain=7  → global_max=15
  Node 20: left_gain=15, right_gain=7 → candidate=42 → global_max=42
  Root:    left_gain=9, right_gain=35 → candidate=34 → global_max=42

Iterative DFS (For Deep Trees):

Idea: Simulate recursion with stack. Track node state (0: unprocessed, 1: left done, 2: both done). Store gains in a dict.

Pseudocode:

def maxPathSum_iterative(root):
    if not root: 
        return 0
    stack = [(root, 0)]  # (node, state)
    gains = {None: 0}    # Handle null children
    global_max = -inf
    while stack:
        node, state = stack.pop()
        if state == 0:      # Unprocessed: push left child
            stack.append((node, 1))
            if node.left:
                stack.append((node.left, 0))
        elif state == 1:    # Left done: push right
            stack.append((node, 2))
            if node.right:
                stack.append((node.right, 0))
        else:               # Both done: compute gains
            left_gain = max(0, gains.get(node.left, 0))
            right_gain = max(0, gains.get(node.right, 0))
            candidate = node.val + left_gain + right_gain
            global_max = max(global_max, candidate)
            gains[node] = node.val + max(left_gain, right_gain)
    return global_max

Complexity: Time ( O(n) ), Space ( O(n) ) (stack + gains dict).

4. Code Deep Dive

Optimal Solution (Recursive):

def maxPathSum(root) -> int:
    global_max = float('-inf')  # Initialize to -∞ for all-negative trees
    
    def max_gain(node):
        nonlocal global_max
        if not node: 
            return 0  # Base case: null nodes contribute 0
        
        # Recurse left/right; clamp negative gains to 0 (skip branch)
        left_gain = max(0, max_gain(node.left))      # Line 7: Skip lossy subtrees
        right_gain = max(0, max_gain(node.right))    # Line 8
        
        # Path through node + both children (cannot extend to parent)
        path_through_node = node.val + left_gain + right_gain  # Line 10
        global_max = max(global_max, path_through_node)        # Line 11: Update global
        
        # Max straight path: node + best child (for parent extension)
        return node.val + max(left_gain, right_gain)  # Line 13
    
    max_gain(root)  # Initiate DFS
    return global_max

Line-by-Line Analysis:

Line 2: global_max = -inf
What: Safeguards all-negative trees.
Why: Single-node paths may be negative (e.g., [-5] → -5).
Lines 7-8: left_gain = max(0, ...), right_gain = max(0, ...)
What: Clamp child gains to 0 if negative.
Why: Negative gains reduce path sum → skip branch.
Line 10: node.val + left_gain + right_gain
What: Path using node + both children.
Why: Captures “bent” paths (e.g., 15→20→7 in Example 2).
Line 11: Update global_max
What: Track best path encountered.
Why: Local paths may be globally optimal.
Line 13: node.val + max(left_gain, right_gain)
What: Max straight path for parent reuse.
Why: Parents can extend this path (no forks).

Edge Case Handling:

All-Negative Tree (e.g., [-3, -1, -2]):
left_gain/right_gain clamp to 0 → path_through_node = -3, global_max updates to -3 at root. Leaf nodes set global_max to max(-1, -2, -3).
Single Node (e.g., [5]):
left_gain = right_gain = 0 → path_through_node = 5 → global_max = 5.
Example 2:
At node 20: left_gain=15, right_gain=7 → path_through_node=42 → global_max=42.
Root: path_through_node=34 < 42 → no update.

5. Complexity War Room

Hardware-Aware Analysis:

Time: ( O(n) ) → 30k nodes = 30k ops (negligible on modern CPUs).
Space (Recursive):
- Worst-case (skewed tree): 30k stack frames.
- Frame size ≈ 128B → 30k * 128B = 3.84MB (fits in L3 cache).
- Risk: Python recursion limit (default 1k) → use sys.setrecursionlimit(35000) or iterative DFS.
Space (Iterative):
- Stack + gains dict: ( O(n) ) → 30k * 64B ≈ 1.92MB (acceptable).

Approach Comparison:

Approach	Time	Space	Readability	Interview Viability
Brute Force	O(n²)	O(h)	★★★☆☆	❌ Fails large n
Recursive DFS	O(n)	O(h)	★★★★★	✅ (if h < 1k)
Iterative DFS	O(n)	O(n)	★★★☆☆	✅ (always safe)

6. Pro Mode Extras

Variants:

Leaf-to-Leaf Max Path (GeeksforGeeks):

Path must start/end at leaves.
Modify: Update global_max only if node has two children.

Code:

if node.left and node.right:  # Only update if both children exist
    global_max = max(global_max, node.val + left_gain + right_gain)

Path Sum III (LC 437):
- Count paths summing to target (not just max).
- Use prefix sums + DFS.
Diameter of Binary Tree (LC 543):
- Maximize edge count (not sum).
- Replace node.val with 1, sum with edge count.

Interview Cheat Sheet:

Key Insight: Path = max(node + best child, node + left + right).
Complexity First: Always state time/space upfront.
Edge Cases:
1. All-negative values.
2. Single node.
3. Skewed trees (recursion depth).
Verification: Test with examples + all-negative.
If Asked: Extend to ( k ) transactions (LC 123) or cyclic graphs.

#124 - Binary Tree Maximum Path Sum

Binary Tree Maximum Path Sum

Problem Description

Solution

1. Problem Deconstruction

2. Intuition Scaffolding

3. Approach Encyclopedia

4. Code Deep Dive

5. Complexity War Room

6. Pro Mode Extras