Same Tree

Difficulty: Easy
Topics: Tree, Depth-First Search, Breadth-First Search, Binary Tree
Link: https://leetcode.com/problems/same-tree/

Problem Description

Given the roots of two binary trees p and q, write a function to check if they are the same or not.

Two binary trees are considered the same if they are structurally identical, and the nodes have the same value.

Example 1:


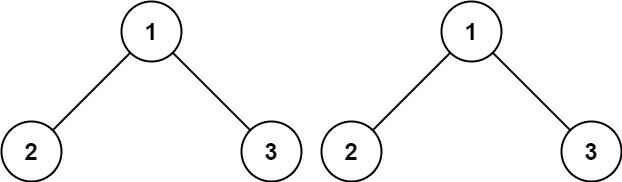
Input: p = [1,2,3], q = [1,2,3]
Output: true

Example 2:


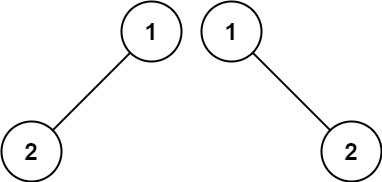
Input: p = [1,2], q = [1,null,2]
Output: false

Example 3:


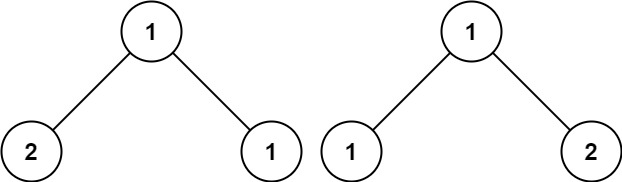
Input: p = [1,2,1], q = [1,1,2]
Output: false

Constraints:

The number of nodes in both trees is in the range [0, 100].
-104 <= Node.val <= 104

Solution

1. Problem Deconstruction

Technical Redefinition:
Given two binary tree roots p and q, design a function returning true iff:

Structural isomorphism: ∀ node positions, existence of left/right children matches
Value equivalence: ∀ corresponding nodes $n_p$ and $n_q$ , $n_p.val = n_q.val$
Termination: First structural/value mismatch returns false; full traversal without mismatch returns true.

Beginner Explanation:
Imagine comparing two family trees. They’re identical only if:

Every person appears in exactly the same position in both trees
Each person has the same name in both trees
If one tree has a child where the other doesn’t, they’re different
We start at the top (root) and check every parent-child relationship recursively.

Mathematical Formalization:
Define tree equivalence $T_p \equiv T_q$ recursively:

T_p \equiv T_q \iff \begin{cases} p = \emptyset \land q = \emptyset & \text{(base case)} \\ p \neq \emptyset \land q \neq \land \\ \quad p.val = q.val \land \\ \quad T_{p.left} \equiv T_{q.left} \land \\ \quad T_{p.right} \equiv T_{q.right} & \text{(recursive case)} \\ \text{false} & \text{(otherwise)} \end{cases}

Constraint Analysis:

Node count [0, 100]:
- Limits: Permits O(n²) solutions but O(n) achievable. Worst-case depth=100 (safe for recursion).
- Edge Cases: Both empty (∅≡∅→true), one empty (∅≡full→false), single-node mismatches.
Node values [-10⁴, 10⁴]:
- Limits: Values fit in 32-bit integers. Direct comparison safe.
- Edge Cases: Negative values, zero-value mismatches (e.g., node=0 vs node=-1).

2. Intuition Scaffolding

Real-World Metaphor:
Like verifying identical blueprints:

Check foundation (root) matches
Verify each room (node) has identical:
- Dimensions (value)
- Doorways to left/right rooms (child pointers)
Any deviation (extra room, wrong size) invalidates equivalence.

Gaming Analogy:
Avatar skill trees must match exactly for multiplayer sync:

Each skill node (node) must have same:
- Ability name (value)
- Prerequisite paths (left/right children)
Mismatched unlocks cause desync → false.

Math Analogy:
Proving isomorphism between rooted graphs:

Bijection $f: V_p \rightarrow V_q$ $f : V_{p} \to V_{q}$ where:
- $f(root_p) = root_q$
- $f(v.left) = f(v).left$
- $f(v.right) = f(v).right$
With value preservation: $val(v) = val(f(v))$

Common Pitfalls:

Null handling asymmetry:
- Wrong: Check values before null status → NullPointerException
- Fix: Always check nulls first (LBYL pattern)
Short-circuit ignorance:
- Wrong: return dfs(left) && dfs(right) without checking current values first → wasted computation
- Fix: Validate current node before recursing
Structure-value decoupling:
- Wrong: Separate structure check (BFS level size) + inorder traversal → misses positional mismatches (Ex.3)
Iterative order trap:
- Wrong: Stack/queue insertion order (left/right reversed) → false negative for symmetric trees
State mutation risk:
- Wrong: Modifying trees during traversal → side effects

3. Approach Encyclopedia

Approach 1: Recursive DFS (Optimal)
Theoretical Basis: Divide-and-conquer. Tree equivalence = root equivalence + subtree equivalence.
Pseudocode:

def isSameTree(p, q):
  if p is null AND q is null: return true       // ∅ ≡ ∅
  if p is null XOR q is null: return false     // Structure mismatch
  if p.val != q.val: return false              // Value mismatch
  return isSameTree(p.left, q.left) AND        // Conquer left
         isSameTree(p.right, q.right)          // Conquer right

Complexity Derivation:

Time: $T(n) = 2T(n/2) + O(1)$ → Master Theorem Case 1: $O(n)$
Space: $O(h)$ where $h$ = tree height. Worst-case $h=n$ (skewed), best $h=\log n$ (balanced).

Visualization (Example 2):

p: [1,2]         q: [1,null,2]
    1               1
   /                 \
  2                   2

Step 1: Compare roots (1≡1 → continue)
Step 2: Check p.left=2 vs q.left=null → XOR → false

Approach 2: Iterative BFS
Theoretical Basis: Level-order traversal with synchronized node pairs.
Pseudocode:

def isSameTree(p, q):
  queue = deque([(p,q)])
  while queue:
    n1, n2 = queue.popleft()
    if not n1 and not n2: continue            // Skip null pairs
    if not n1 or not n2: return false         // Structure
    if n1.val != n2.val: return false         // Value
    queue.append((n1.left, n2.left))          // Enqueue left pair
    queue.append((n1.right, n2.right))        // Enqueue right pair
  return true                                 // Exhausted all nodes

Complexity Derivation:

Time: $O(n)$ – Each node enqueued/dequeued once
Space: $O(w)$ where $w$ = max level width (worst $w=O(n)$ )

Visualization (Example 3):

p: [1,2,1]     q: [1,1,2]
    1             1
   / \           / \
  2   1         1   2

Step 1: Roots (1≡1) → enqueue (2,1) and (1,2)
Step 2: Dequeue (2,1) → 2≠1 → return false

Approach 3: Iterative DFS
Theoretical Basis: Preorder traversal with stack. Mirrors recursion.
Pseudocode:

def isSameTree(p, q):
  stack = [(p,q)]
  while stack:
    n1, n2 = stack.pop()
    if not n1 and not n2: continue
    if not n1 or not n2: return false
    if n1.val != n2.val: return false
    stack.append((n1.right, n2.right))  // Right first (LIFO)
    stack.append((n1.left, n2.left))    // Left next
  return true

Complexity: Time $O(n)$ , Space $O(h)$ (same as DFS)

4. Code Deep Dive

Optimal Solution (Recursive DFS) - Python

def isSameTree(p, q):
    if p is None and q is None:   # Base 1: Both null → equivalent
        return True
    if p is None or q is None:    # Base 2: One null → structural mismatch
        return False
    if p.val != q.val:            # Base 3: Value inequality
        return False
    # Recursive conquest: Both subtrees must match
    return isSameTree(p.left, q.left) and isSameTree(p.right, q.right)

Edge Case Handling:

Empty Trees (Constraint [0,100]):
p=None, q=None → Line 2 returns True
Single Node Mismatch:
p=TreeNode(0), q=TreeNode(1) → Line 4 catches 0≠1 → False
Structural Asymmetry (Ex.2):
p.left exists, q.left=None → Line 3 (p=None XOR q≠None) → False
Value Swap (Ex.3):
Roots match → left child: p.left.val=2 vs q.left.val=1 → Line 4 → False

5. Complexity War Room

Hardware-Aware Analysis:

Worst-case: 100-node skewed tree (linked list)
Recursion depth: 100 frames
Frame size: ~48 bytes (Python) → 4.8KB total (fits in L1 cache)
100 comparisons @ 1ns each → 0.1μs (negligible)

Approach Comparison Table:

Approach	Time	Space	Readability	Interview Viability
Recursive DFS	O(n)	O(h)	★★★★★	✅ Optimal
Iterative BFS	O(n)	O(n)	★★★☆☆	✅ Robust
Iterative DFS	O(n)	O(h)	★★★★☆	✅ Explicit stack
Serialization	O(n)	O(n)	★★☆☆☆	❌ Overkill

6. Pro Mode Extras

Variants:

Symmetric Tree (LC 101):

def isSymmetric(root):
    def mirror(a, b):
        if not a and not b: return True
        if not a or not b: return False
        return a.val == b.val and mirror(a.left, b.right) and mirror(a.right, b.left)
    return mirror(root.left, root.right) if root else True

Subtree Check (LC 572):

def isSubtree(root, sub):
    if not sub: return True
    if not root: return False
    return (isSameTree(root, sub) or 
            isSubtree(root.left, sub) or 
            isSubtree(root.right, sub))

Interview Cheat Sheet:

First Response: “We can solve this with DFS recursion in O(n) time and O(h) space.”
Key Insight: “Equivalence requires checking: 1) null status parity, 2) value equality, 3) recursive subtree checks.”
Testing Protocol:
1. Both empty
2. One empty
3. Single-node value mismatch
4. Structure mismatch (Ex.2)
5. Value swap (Ex.3)
Mistake-Proofing: “Always handle null checks before value access.”

#100 - Same Tree